main05

One could use graphs to illustrate ordering relations, as well as other relations. Such a graph would contain too many edges and self-loops (as a consequence of reflexivity). It is more convenient and clearer to present an ordering relation by a Hasse diagram.

Definition 5.2.1

A Hasse diagram of an ordering relation ≤ in a set X is a directed graph G = <X, E> where the set of nodes is the set X and the set of edges is defined as follows

(x,y) ∈ E iff x ≤ y and there is no z ∈ X, such that z ≠ x, z ≠ y and x ≤ z and z ≤ y .

We say that an element y is the direct successor of an element x if the pair (x,y) is an edge in the Hasse diagram.

In a Hasse diagram, we draw line segments instead of arrows, usually connecting elements of directed graphs. We take care to make sure that the end of an edge is placed higher on a diagram than its beginning. Whenever y is a direct successor of x in a Hasse diagram line segment connecting x and y is directed upward from x to y.

Fig. 5.2.1 Diagram of Hasse (a) of inclusion relation in the set of all subsets of the set {R, G, B}, (b) of the divisibility relation in the set {1, 2, 3, ...,9}.

(1) Relation ⊆ of inclusion in the set of all subsets of a certain set X is the partial ordering relation. Inclusion relationis reflexive since A ⊆ A. It is an antisymmetric relation because A ⊆ B and B ⊆ A implies A=B. The relation of inclusion is transitive because A ⊆ B and B ⊆ C imply A ⊆ C (c.f. 1.2).

Remark: There are sets in P(X) which cannot be compared by the relation ⊆. Let x and y be distinct elements of set X,then {x} ∈ P(X), {y} ∈ P(X), however, neither {x} ⊆ {y}nor {y} ⊆ {x}.

Hasse diagram of the relation ⊆ in the case when X = {R, G, B} is shown on Figure 5.2.1(a).

(2) The divisibility relation | defined on the set N of natural numbers by the formula

is an ordering relation. Indeed, the divisibility relation is reflexive, antisymmetric and transitive. Figure 5.2.1(b) illustrates the graph of this relation restricted to the subset {1, 2, 3, ...9}. Figure 5.2b Hasse diagram of this relation. As in the preceding example, we observe that this is a partial ordering because there are numbers which cannot be compared by the relation |. For example, 2 is not a divisor of 3 and 3 is not a divisor of 2. So there is no line segment between 2 and 3.

(3) Let Σ = {0, 1}. We define a relation ≤ in the set Σ* (the set of all words over the alphabet Σ) :

The word ww" is the result of putting the word w" after the word w. This operation is called concatenation. For example the concatenation of words "abcd" and "efgh" gives the word "abcdefgh".

If w' ≤ w, we say that the word w' is an initial segment or a prefix of the word w. The relation ≤ in the set {0,1}* defines a partial order. Hasse diagram of this order is limited to a few cases, c.f. Figure 5.2.2. The set {0,1}* is an infinite set.

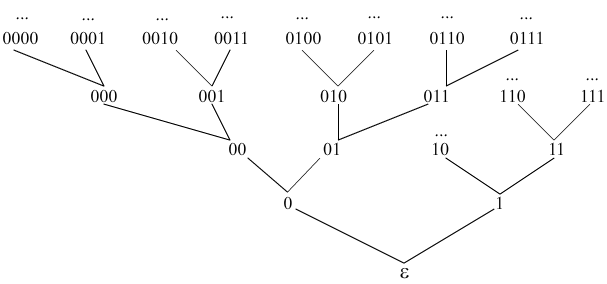
Fig. 5.2.2 A fragment of the Hasse diagram of partial ordering in the set of words over the alphabet {0,1}, c.f. example 5.2.1(3).