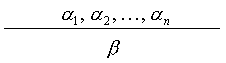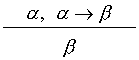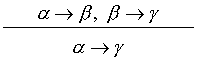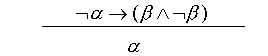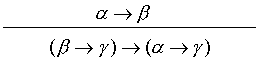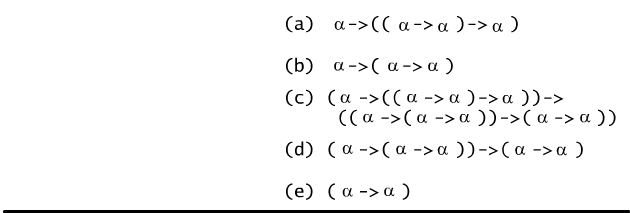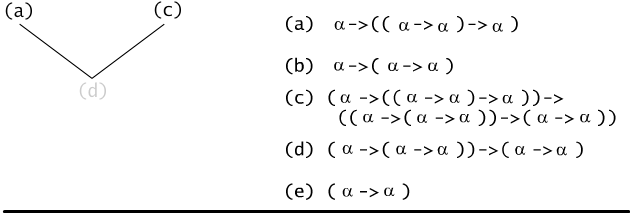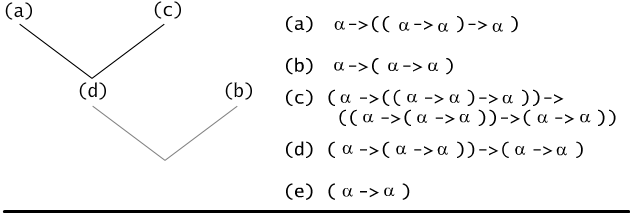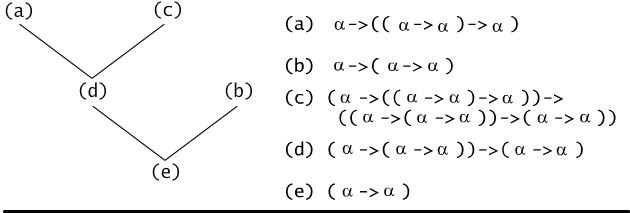6.6 Rules of inference
The main role of propositional calculus is to provide us with tools
which
allow to
construct and to analyse deductive
reasoning. On what does such reasoning depend? How does this reasoning
work? We start with previously
proved propositions (formulas) or with propositions generally assumed
to be true (axioms). Then, using easy
transformations, we try to deduce other propositions. These
transformations
are
called inference rules. Before we give a more exact definition
of a deductive process, let's consider two examples.
Example 6.6.1
Let us assume that the following two propositions are true
- I like Kate or Ann.
- If I do not like Kate, then I do not like Ann.
Does it follow necessarily that I like Kate or necessarily follows
that I like Ann?
Let's analyse this situation more precisely. Assume that p = "I like
Kate" and q = "I like Ann". According to the assumptions (a) and
(b) both
propositions (p ∨ q) as well as ( ¬ p ⇒ ¬ q) are true,
i.e.
(p ∨ q)(v) = 1 and ( ¬p
⇒ ¬q)(v) = 1.
If v(p) = 0, then using the first assumption (a) we obtain v(q) = 1
but this time (q ⇒ p)(v) = 0, contrary to
the
second assumption (b). Hence, it follows from satisfiability of
the propositions (a) and (b) that the proposition "I like Kate" must be
true. The proposition
q may be false or true.
Example 6.6.2
Let us assume that someone has asked me:
"Is it true that if you like Kate,
then you like Ann too?"
I have answered:
"If it is true, then I like
Kate".
Can we conclude form this conversation whether I like Kate?
Let us use the previous example's notation. Let v describe my
feelings, i.e. v gives the values of p and of q. The question can
be reworded as whether the formula (p ⇒
q) is true at the valuation v. Hence,
according to the answer we have ((p ⇒ q) ⇒ p)(v) = 1. Now, if v(p) = 0, then we have
(p ⇒
q)(v) = 1, but then ((p ⇒ q) ⇒ p)(v) = 0, contrary to the assumption.
Thus, we
can conclude from the conversation that v(p)=1, and therefore,
the
answer to the question is affirmative: "Yes, I like Kate". ♦
In the examples presented above, in order to find out the final
conclusion from the approved assumptions, we have analysed different
cases to
check in a semantic way whether they can or cannot occur. Rules of
inference
are general
schemes of the formal process which allows to reach a conclusion,
without calling to the semantics and to the interpretation
of variables every time. They establish syntactic relations between a
finite
set of formulas called premises and a formula called
a conclusion. The application of a rule of inference is a purely
syntactic procedure. Nevertheless it must also be correct, or more
precisely validity preserving.
Definition 6.6.1
The
rule of inference is a scheme of the form:
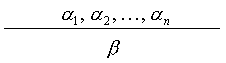
which any finite set of formulas α1,
..., αn, called
premises, assigns the formula β,
called the
conclusion, in such a manner that, if all premises are true, then the
conclusion is also
a true proposition. We say that β
is a logical consequence of the formulas α1,...,
αn.
More formally, the scheme presented above is a correct rule of
inference iff α1(v) =
1,..., αn(v) = 1 implies β
(v) = 1 for every valuation
v of propositional variables.
Example 6.6.3
(a) The important example of an inference's rule is the rule of
modus
ponens,
in short m.p.:
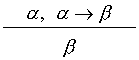
Let us check this rule correctness. Let α(v)
= 1 and ( α
®
β)(v) = 1 for some arbitrary
valuation v.
According to the semantics of implication and keeping in mind
that α(v) = 1, we obtain β(v) = 1. ♦
(b) The other example of a rule of inference is the rule of
conditional syllogism:
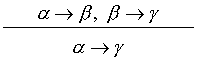
We want to prove that it is a correct inference rule.To this aim,
let us
assume that for a valuation v, ( α
→ β)(v) = 1 and ( β →
γ)(v) = 1. Now we need to consider two
cases:
- α(v) = 1. Then β(v)
= 1, by the first assumption. Thus from the second assumption γ(v)
= 1 but then we have also
( α → γ)(v) = 1.
- α(v) = 0.
Then, regardless of the value of βand γ, we obtain ( α
→ γ)(v) = 1. ♦
(c) Our third example of inference's rule is the scheme which is
often applied
in the proofs by contradiction ("reductio ad absurdum"), see. section
6.5.
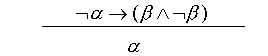
If we assume that ( ¬
α
→ ( β ∧
¬
β
))(v) = 1 for some valuation v, then the
only possibility is that ( ¬
α)(v) = 0. It follows that α(v) = 1. ♦
Question 6.6.1 Is the following scheme a correct rule of
inference.
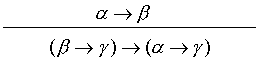
-----
Check the Answer -----
Problem 6.6.1
Assume that there exists a country in which live only
true-speaking or false-speaking natives. Furthermore, if you ask them
any question, they answer shortly YES or NO. Some hungry tourist comes
to the road fork where are exactly two new roads. One of them leads to
the restaurant while the other does not. Because there are no
restaurant-leaded road signs, tourist decides to ask a met native which
way he ought to go. How the tourist should construct his question in
order to chose a proper way to the restaurant?
Answer: We want to build question in such a manner that
regardless of true-speaking or false-speaking native the answer YES
means
that the tourist should go along the left road and the NO answer
means that
tourist should go along right road. Let p denotes type of native:
p = 1 - true-speaking, p = 0 -
false-speaking,
and q determines a choice of road leading to the restaurant:
q = 1 - left road leads to the
restaurant, q = 0 - right road leads to the restaurant.
It follows that the question x, which tourist ought to ask,
has logical matrix as presented below
|
p
|
q
|
x
|
|
1
|
1
|
1
|
|
1
|
0
|
0
|
|
0
|
1
|
0
|
|
0
|
0
|
1
|
If the tourist meets a trueth-speaking native then he should obey
the
native's
answer (variable q). On the other hand, if the tourist meets
a false-speaking one,
then he should not obey the native's answer (negation of the variable
q).
It follows from the presented logical matrix that the tourist's
question ought
to have the form (p ∧
q) ∨ ( ¬
p ∧
¬
q). Therefore the final question is: "Is the following question true:
'You are a truth-speaking person if and only if the left road leads to
the
restaurant"".
There is a very close relation between rules of inference and
propositional calculus tautologies. Rules always lead from tautologies
to tautologies. What is more, every tautology written down in the form
of
an implication may be transformed into the correct rule of inference
and
conversely, every correct rule of inference corresponds to a
tautology. This relationships are expressed in the next two lemmas 6.2
and 6.3.
Lemma 6.6.1
If all premises of a rule of inference are tautologies, then
the rule's conclusion is also a tautology.
Lemma 6.6.2
Let α
1,..., α
n, β be propositional calculus
formulas. The proposition ( α
1 ∧
... ∧ α
n) → β
is a tautology if and only if
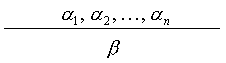
is a correct rule of inference.
Rule of inference allows us to deduce new tautologies from others
checked before. Thus, there arises a question if we can construct
a logical system which consists of a small number of tautologies and
rules of inference which lets us derive all other possible tautologies
of
propositional calculus. This approach is called axiomatic and the
answer to this question is positive.
Many different axiomatic systems of propositional calculus exist. We
will outline a standard system which consists of four schemes of
tautologies (we call them axioms of propositional calculus), see Fig.
6.6.1, and the only rule of inference - modus ponens.
|
α → (β → α)
|
a rule of simplification,
|
|
¬ α → (α → β
)
|
a rule of Duns Scotus,
|
|
( ¬ α → α) → α
|
a rule of Clavius,
|
|
(α → (β → γ)) → ((α → β) → (α → γ))
|
a rule of Frege.
|
Fig. 6.6.1 Propositional calculus axioms.
Below we present the precise definition of proving process, i.e. the
concept
of a propositional calculus formal proof.
Definition 6.6.2
A finite
sequence of formulas α1, ..., α n is called a proof of the
formula α if and only if every
formula αi (i=1,2...n) is either
an axiom or is a conclusion in the rule of modus ponens in which the
premises
are formulas αk and αj where k and j are less than i
and α j = ( αk → αi).
Example 6.6.3
The following sequence of formulas is a formal proof of the formula (α →
α).
- ( α →
(( α → α) → α)) (a tautology of
the form (a → (b →
a)), law of simplification)
- ( α → ( α → α))
(law of simplification)
- ( ( α →
(( α → α) → α)) → (( α →
( α → α)) →
( α → α))) (law of
Frege
((a →
(b →
c)) →
((a →
b) →
(a →
c))) )
- (( α → ( α → α)) →
( α → α)) (form (a) and
(c) by applying modus ponens rule)
- ( α → α)
(form (d) and
(b) by applying modus ponens rule).
Remark. We usually do not derive formal proofs. The most
important is that, if it is necessary, we may carry out formal
reasoning
and make its detailed analysis step by step.
It is quite natural to write down a formal proof as a binary tree
(see Fig. 6.6.2). The label of the root of such a tree is just the
proven formula, the labels of the leafs are axioms used during the
proving process. All internal vertices' labels are obtained by
applying the rule of modus ponens:
if x is a vertex which successors are labeled by γ and ( γ → β), then x
is labeled by β.
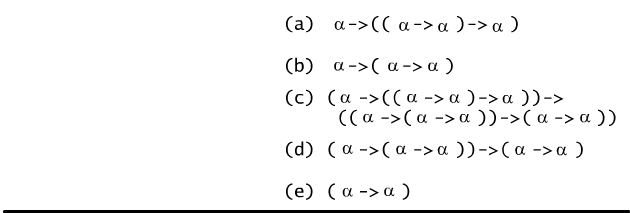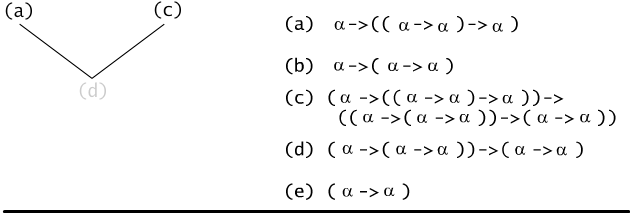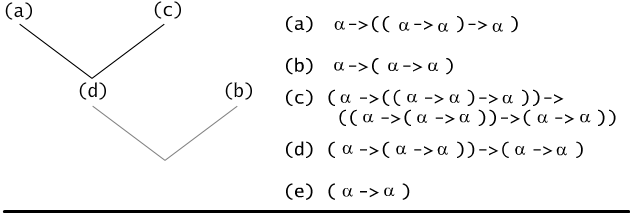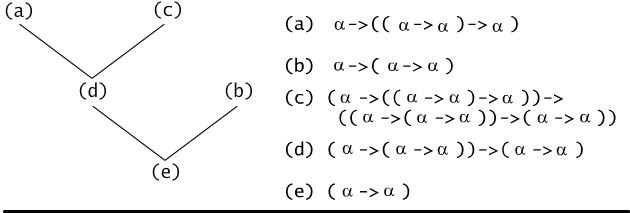
Fig. 6.6.2 The tree of the formal proof of the formula ( α
→
α).
To finish off we note that the axiomatic system of propositional
calculus has the property of completeness,
i.e.
all what we can prove in
this system is always true and every proposition which is true may be
proved in this system. In this way we obtain one more method of proving
tautologies - a formal method. One should not assume that this
solution
is less time-expensive than the 0-1 method. Finding out a formal proof
needs
much more ingenuity and a applying a computer takes the same amount of
time
as the 0-1 method.