In lecture 3 we introduced infinite sequence as a total function defined over the set of natural numbers N. To describe the elements of this sequence, it is convenient, to use an inductive definition. This method consists of two steps:

- characterise the first or the first few elements of the sequence,

- define how to construct the (n+1)-th element depending on the n-th element or other already defined elements.

Let's look at the following examples:

Example 8.4.1

(1) We are given the characteristics of the sequence (a_i)_{i ∈ N} :

a₀ = 1, a_n+1 = a_n + 2 for every n ≥ 0.

It is easy to calculate that a₁ = a₀ + 2 = 1+2 = 3, a₂ = a₁ +2 = 5 etc. If we look closer at the relations of these elements we conclude that a₁ = a₀ + 2 = 1+ 1 ⋅2 , a₂ = 1 +2 ⋅2 = 5, a₃ = 1 +2 ⋅2 +2 = 1 +3 ⋅2.

Of course, we may guess that a_k = 1+ k ⋅2 for all k>0. In order to prove this observation (i.e. a_k = 1+ 2k for every natural number k) we use the induction principle. Thus, the case in which k=0 (induction basis) is obvious, a₀ = 1. The induction step is a result of the induction definition of considered sequence, as well as the induction assumption for some arbitrary k: a_k+1 = a_k + 2 = (1+ 2k) + 2 = 1+ 2(k+1).

(2) We are given a characteristic of sequence b = (b_i) _{i ∈ N} :

b₀ = 1, b₁ = 1, b_n+1 = b_n ⋅ (n+1) for every n ≥ 0.

A few first elements are:

b₁ = b₀ ⋅ 1 = 1, b₂ = b₁ ⋅2 = 2, b₃ = b₂ ⋅ 3 = 6, b₄ = b₃ ⋅4 = 24, etc.

With no effort we can prove that b_n = 1 ⋅2 ⋅3 ⋅... ⋅n = n!

Problem 8.4.1 Using the induction principle prove that the n-th element of the sequence b from example 8.4.1 has a form b_n = n!

------Check the answer -----

Let us take a sequence described with the following inductive definition

f₀ = 0, f₁ = 1, f_n+2 = f_n + f_n+1

This sequence is called the Fibonacci sequence.

Of course, using the definition presented above, we can easily calculate the values of the set's elements. This task requires regularity of calculus as well as our patience. For example for f₇ we obtain f₇ = f₅ + f₆ = f₅ + f₄ + f₅ = 2(f₃ + f₄ ) + f₄ = 3(f₂ + f₃) + 2 f₃ = 5(f₂ + f₁) + 3f₂ = 8(f₀ + f₁ )+ 5 f₁ = 13.

Now we prove by the mathematical induction principle that for every natural number n, it holds that:

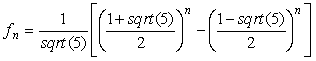
Induction basis. If n=0, then the right side of the above equation amounts 0 as well as f₀ = 0 form induction definition.

Induction assumption. Assume that this formula is valid for all natural numbers smaller than k+2.

Induction thesis. Considered equation is correct for k+2.

Thesis' proof. To simplify our task we introduce the following notation

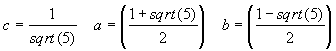
Now induction thesis can be rewritten in the form of  f_i = c(aⁱ -bⁱ) for i <k+2. Therefore, if we use this formulas for k, k+1 and we take the induction definition of Fibonacci sequence then:

f_k+2 = f_k + f_k+1 = c(a^k -b^k) + c(a^k+1 -b^k+1) = c [a^k (1 + a) - b^k(1 + b)]

Because 1+a = a², a 1+b = b², thus f_k+2 = c(a^k+2 -b^k+2).

According to the induction principle every element of Fibonacci sequence may be expressed by the above formula. ♦

Let us take a sequence a₀, a₁, a₂,..., the elements of which are natural numbers. A sum of the first n-th elements of this sequence we denote by

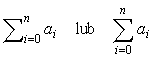
and read "sum of a_i for every i from 0 up to n". If we do not sum all sequence elements but only an arbitrary subsequence or elements which satisfy a special condition w, we write

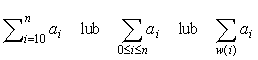
This notation is unambiguous and more comfortable than the classical one (i.e. a₀ + ... +a_n), which does not tell us the meaning of dots straight out. Can you guess what is the next number in the sequence 0,1,1,2,3,...?

Of course, we do not care about the index letter, i.e. the  symbols of the following sum have equal meaning:

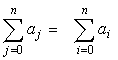
Similar notation may be introduced for product operator. The product of (n+1) elements of the sequence (a_i)_{i ∈ N} is denoted by a classical form a₀ ⋅ ... ⋅a_n or by the following symbols:

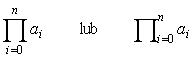
Question 8.4.1 What are the exact values of the following expressions:

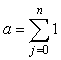
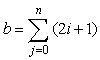
Example 8.4.3

Let's consider the following sequence consisting of numbers: a₁ = 1, a_n = a_n-1 + 1. Now we construct a new sequence b, the n-th element of which is a sum of the first n elements of the set (a_i) _{i ∈N}, i.e. b₁ = a₁, b_n = a₁ +...+a_n. The elements of this sequence are called triangular numbers (in order to know why, see fig. 3.1.3). Of course, for any i, a_i = i (this conclusion can be easily proved by induction). Next elements of sequence b take values: b₁ = 1, b₂ =3, b₃ = 6, b₄ = 10, b₅ = 15. We prove that

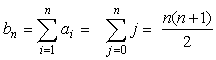
Proof.

In the n=1 case we obtain (1+1) ⋅1/2 =1, thus the formula is valid for n=1 (induction basis).

Let's assume that the formula is satisfied for some n=k, i.e.

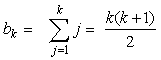
Using this assumption, as well as the inductive definition of the sequence b, we may do the following transformation

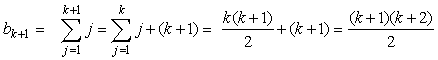
It follows that, in agreement with the induction principle, every element of the sequence b has a form b_n = n(n+1)/2.

Question 8.4.2 What is the value of the product of  the first  n elements of the sequence a₀ = 2, a_i+1 = 4a_i for i>0?

Problem 8.4.2 Prove by induction that the sum of the first n elements of the  sequence defined by

amounts 2ⁿ -1.

Hint: Show that the n-th element of the sequence can be described by the formula a_n = 2ⁿ  and then, using induction reasoning on number of sum's elements, prove that 1 + 2 + ...+ 2^n-1 is equal to 2ⁿ -1.

« previous section

next section »