« previous section    next section »


8.5 Recursion

In the previous subsection of this lecture we focused on inductive definitions of infinite sequences. Now we want to continue the presentation of this implicite manner of defining, not only one-argument but also many-argument functions. The method is called defining by recursion. How does it work? The general idea is easy: in order to define the value of an operation for some arguments we use values of the same operation for other more basic arguments. Therefore, the large problem's solution is reduced to solutions of a few arbitrary smaller problems.

Example 8.5.1

(1) Addition over the set of natural numbers with zero and the successor function (according to Peano's axioms) may be defined in the following way:

n + 0 = n, for every n ∈ N,

n + suc(m) = suc(n + m) , for every n, m ∈ N.

Using this definition, as well as Peano's axioms, we can prove all well-known properties of sum operation, e.g. commutability, connectivity etc.

(2) Multiplication over the set of natural numbers may be defined in a similar way:

n ⋅ 0 = 0, for every n ∈ N

n ⋅ suc(m) = (n ⋅ m) + n, for every n, m ∈ N.

Using this definition as well as Peano's axioms we can prove that the product operator is a well-defined operation for every pair of natural numbers. Of course, we are able to show all other properties of this operator.

We give as an example the inductive proof for the law of distributivity.

Lemma 8.5.1

For every natural numbers m, n, k, it holds that

(m + n) ⋅ k = m ⋅ k + n ⋅ k.

Proof.

Let m and n be arbitrary natural numbers. We denote the above formula with the F(k) symbol.

If k=0, then (m+ n) ⋅ k =(m+ n) ⋅ 0 = 0 and, according to the recursive definition of multiplication,  m ⋅ k + n ⋅ k = m ⋅ 0 + n ⋅ 0 = 0+0. Now from the definition of addition we derive 0+0 = 0 that is F(0).

Let's assume that the lemma's formula  F is valid for some k, i.e. we assume the correctness of F(k). By the terms of the definition of addition and of multiplication operators, as well as laws of  commutativity and associativity, we obtain

(m + n) ⋅ suc(k) =(m+ n) ⋅ k + (n + m) = (m ⋅ k + m) + (n ⋅ k+n) = m ⋅suc(k) + n ⋅suc(k).

Thus, according to principle of mathematical induction, for any natural number k, F(k)holds. It follows that the law of distributivity under  consideration is complied with for every natural numbers m, n, k.

Question 8.5.1 Give the recursive definition for the operation of exponentiation in the set of natural numbers.

Recursive definitions are often used in computer programming. It is because recursion-based implementations of many problems are shorter and more legible than non-recursive ones. Look below at the examples.

Example 8.5.2 Euclid's algorithm

Denote by gcd(n,m) the greatest common divisor for numbers n and m. The mathematical definition of this two-argument operation can be given in the following way:

gcd(n,m) = k ≡ (k|n ∧ k|m) ∧ ( ∀ x) ((x|n ∧ x|m ) → x|k)

It is a trivial task to find (by prime factoring) the value of gcd for arbitrary not large numbers, e.g. gcd(4,6)= 2, gcd(12,6) = 6, gcd(36,27)= 9 etc. Unfortunately, this method cannot be applied to significantly larger numbers (we do not know any effective algorithm for the factorisation problem). But our situation is not so bad as it seems to be thanks to some mathematical facts:

gcd(x,y) = gcd(y,x), gcd(x,0) = x,

gcd(x,y) = gcd(y, x mod y), where y ≠ 0 and x ≥y,

gcd(x,y) = gcd(x, y - x), where y>x,

gcd(x,y) = gcd(x - y, y), where x>y.

 These characteristic of the greatest common divisor operation imply easy algorithms (gcd1 or gcd2) which calculate gcd for any arbitrary x, y ∈ N.

gcd1(x,y) {
 if x = y then return x
  else if y>x then return gcd1(x, y - x) else return gcd1(x - y, y) fi
 fi
}

gcd2(x,y) {
 if y=0 then return x else
  return gcd2 (y, x mod y) fi
}

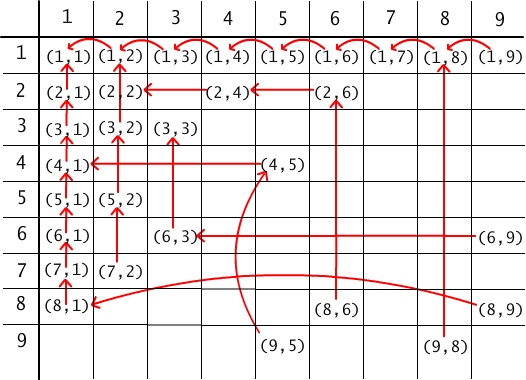
Algorithms gcd1 as well as gcd2 are recursive procedures. In order to calculate the value of gcd for x and  y we need to find (using the same procedure) the values of the gcd operation for other arguments, i.e. we are calling recursively the same procedure in its body. The examples of chains of successive recursive procedure calls for the gcd1 algorithm are presented on Fig. 8.5.1

Fig. 8.5.1 The chains of recursive calls of the procedure gcd1.

Example 8.5.3 Graph travelling.

Let us take a binary tree G with the root in the vertex r (see fig. 8.5.2). Let for every vertex x of this tree two functions left(x) and right(x) be defined, the values of which are vertices being adequately left or right successors of x, or,  a special value none when vertex x have no immediate successors. Let's assume that r ≠ none. The following procedure GO is a recursive method for visiting all G tree's vertices.

GO (G,x){
  if x ≠ none then
    visit(x);
    GO(G, left(x));
    GO (G, right(x));
  fi; }

If we call this procedure for the tree G, as it is shown on Fig. 8.5.2 and value x=R, then the tree's vertices should be visited in the following order: RALIVOEGLOTICMHIS.

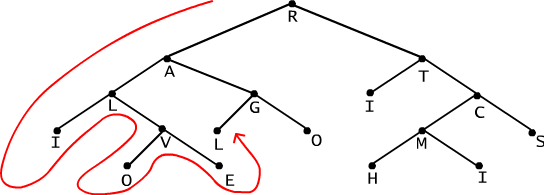
Fig. 8.5.2 Visiting tree's vertices. Result vertex ordering for procedure GO: RALIVOEGLOTICMHIS.

Question 8.5.2 What is the vertices order of vertices for the modified version of the procedure GO, GObis,

GObis(G,x){if x ≠ none then GObis(G, left(x));  visit(x); GObis(G, right(x)); fi;},

 applied to the graph on Fig. 8.5.2?

Problem 8.5.1 Check GO procedure results for other examples of trees.

Potential troubles: Presume that we introduce a recursive definition for some operation over the set of natural numbers in the following manner:

something(x,0) = 0,

something(x,y+1) = something(x,y+1)+1.

This definition cannot be accepted. We never find a value of something(x,y+1) because this expression appears both on the left as well as the right side of a recursive formula. If we adopt that something(x,y+1) is equal to an arbitrary a, then we receive a contradiction 0=1.

To avoid this problem a recursive definition should have the following form

h(x,0) = f(x)

h(x,y+1) = g(x,y,h(x,y))

for some functions f(x) and g(x,y,z).

It is worth remembering the above schema especially when we implement the body of a function in a very involved manner (i.e. we repeatedly call to the implemented function and others).

Question 8.5.3 Give a recursive definition for the operation min which finds the minimum in the sequence of real numbers a[0], a[1],..., a[n].


« previous section    next section »