We say that a set is finite, if the number of its elements amounts to n, where n is a natural number. When two finite sets have the same number of elements we say they have the same power, or that they are equipotent. 

The concept "the same number of elements" ceases being intuitive if it applies to infinite sets. For example, let's consider two sets: the set of natural numbers and the set of all natural numbers greater than 100. Do they have "the same number of elements"? There are several elements in the first set that do not belong to the second set.  Is it important?

Observe that, when two finite sets store the same number of elements then we may determine a one-to-one function  which transforms one set onto the other one (i.e. we can construct a bijection). This function can be created by building separate sequences of elements of both sets and  ascribing the i-th element of the first sequence to the i-th element of the second sequence (see lecture 3). The existence of a bijection from one set to another intuitively illustrates the problem of sets equipotency: yet, using this function we paired all sets' elements in such a manner that every pair's predecessor belongs to the first set and every pair's successor belongs to the second set and moreover each sets' element appears exactly once. 

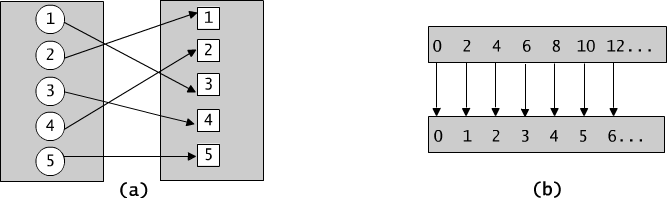
Fig. 9.1.1 (a) Function establishing the equipotence of the sets of circles and squares. (b) Function establishing the equipotence of sets of even and of natural numbers.

Example 9.1.1

1. On Figure 9.1.1 we presented two simple examples of equipotent sets. Both, the set of circles as well as the set of squares, store the some number of elements (see Fig. 9.1.1(a)). This property can be easily checked by counting elements, as both sets are finite. The function, described with arrows on Figure 9.1.1(a), is one of one-to-one correspondence form one set onto another. If the first set has three elements and the second  five,  then no such function could be found. In this case the sets are not equipotent. The concept of equipotent sets is, in the case of finite sets, identical to the idea of having the same number of elements.
   
   
2. The sets presented on Figure 9.1.1(b) are infinite. Of course, the set of even numbers, P, is a proper subset of the natural numbers' set, N. Nevertheless, the function f(x) = x div 2 is a bijection form P onto the set of natural numbers. This function determines equipotence of P and N.
   
   
3. Any two intervals of real numbers are equipotent. On Figure 9.1.2(a) we introduce the linear function f(x) = (x-a)(d-c)/(b-a)+ c which is one-to-one assignment from the  interval [a, b] onto the interval [c, d].

Fig 9.1.2 (a) The function which determines equipotence of intervals [a,b], [c,d]. (b) Trigonometric tangent function which determines equipotence of the set of real numbers and the open interval (-pi/2, pi/2).

Question 9.1.1 Give a function which establishes equipotence of the set N and the set N\{0,1,2,3,...,100}. Write down the simplest possible correspondence.

Proof.

Ad(1) If A ~ B then there exists a one-to-one function form the set A onto the set B. According to the definition (see section 3.3) there  exists its inverse function, which is a bijection form A onto B, that is B ~ A.

Ad(2) Providing that the first assumption (A ~ B) is satisfied there exists bijection f : A → B. According to the second assumption (B ~ C) there exists bijection g: B → C. Because the composition of the functions f and g,  f ° g, is a bijection   which maps the  set  A onto the set C (see Lemma 3.3.2), therefore A ~ C.  ♦

Now, using lemma 9.1.1, we prove a bit surprising theorem that all real numbers "can be fitted" into a freely small interval of real numbers.

Proof.

In order to achieve our goal we use functions described on the Figure 9.1.2. Firstly, the tangent function is one-to-one correspondence which maps the open interval (-pi/2, pi/2) onto R. That is (- pi/2, pi/2) ~ R. Furthermore, the linear function, described on Figure 9.1.2(a), allows to project any open interval e.g. (a, b) where a < b, onto the interval (-pi/2, pi/2). Hence (a, b) ~ (- pi/2, pi/2). Hence, according to lemma 9.1.1, the sets (a, b) and R are equipotent. ♦

Question 9.1.2 Are the sets X = { x ∈ N: 0 ≤ x<10 } and Y = { x² : x ∈ N and x is even number less then 20} equipotent?

« previous section

next section »