Remark. Using this definition we may conclude that an arbitrary set is at most countable if all its elements can by lined up in a sequence in which every element appears exactly once.

Example 9.2.1

(1) The set of even numbers is enumerable, see Figure 9.1.1(b).

(2) The set of odd numbers is enumerable because, e.g. function f(x) = 2x+1 is a bijection which maps the set of natural numbers onto the set of odd numbers.

(3) The set of all integer numbers is enumerable because the function f defined conditionally as f(x) = 2x-1 for x>0 and f(x) = -2x for x ≤ 0 is a one-to-one mapping of the set of integer numbers onto the set of natural numbers (it transforms positive integer numbers to odd numbers and negative as well as zero to even numbers).

Proof.

Because every subset of a finite set is a finite set, thus in this case, lemma 9.2.1 is obvious. Let X be an enumerable, infinite  set, f - a bijection such that  f : N → X and A - an infinite subset of the set X. The function f allows us to line up elements of the set X in a sequence (f(i))_{i ∈N}. If we remove from this sequence the elements which do not belong to A, then we obtain the infinite sequence of elements of the set A.

Let's define a function g : N → A in such a way that successive natural numbers are ascribed to next not removed and not used  elements of the set A (see Fig. 9.2.1).

g(0) = f(k₀), where k₀ = min{i : f(i) ∈ A}

g(1) = f(k₁), where k₁ = min{i : f(i) ∈ A\ {g(0)}}

g(2) = f(k₂) ), where k₂ = min{i : f(i) ∈ A\ {g(0), g(1)}} etc.

g(j) = f(k_j) ), where k_j = min{i : f(i) ∈ A\{g(0), g(1),...,g(j-1)}}

The set {i : f(i) ∈ A\{g(0), g(1),...,g(j-1)}} is non-empty for every j (in the other case the set A would be finite). Furthermore, because natural numbers' set as well as all its subsets are well-founded (see subsection 5.6), there always exists the smallest element in any of these sets. Thus, the definition of  g is correct. The function g is a mapping "onto" the set A (every element of the set A appears on some position e.g. j-th in the sequence (f(i))_{i ∈N}). Therefore, after j steps it must be chosen as a value of the function g. The construction of  g implies that g is a one-to-one function. Thus, it establishes equipotence of sets A and N. ♦

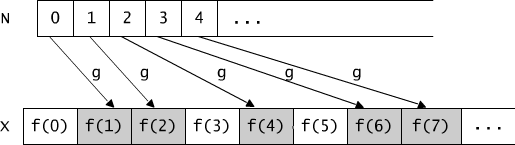
Fig. 9.2.1 A mapping of the set of natural numbers onto an infinite subset of some arbitrary set X. The gray-boxed elements of set X correspond to elements of the set A.

Conclusion. Intersection of at most countable sets is also an at most countable set.

Question 9.2.1 The intersection of a countable set and a finite set is countable or finite ?

Proof.

Ad 1. Let X and Y are infinite countable sets. Thus, the elements of these sets may be lined up in sequences. Assume that X = (x_i)_{i ∈N} as well as Y = (y_i) _{i ∈N}. Let f be a function which maps N onto X ∪ Y in such manner that even numbers are ascribed to elements of the set X and odd numbers are ascribed to the elements of the set Y. This process creates an infinite sequence of elements of the set X ∪ Y. If the intersection of the sets X and Y is non-empty then some elements appear twice. Now, if we remove every one of doubled elements and, if need be, re-ascribe remaining sequence's elements, then we construct a function which is a bijection of the set N onto the set X ∪ Y. Thus, the union  X ∪ Y is  an enumerable set (see Figure 9.2.2).

If both X as well as Y are finite then their union is also a finite set. If one of these sets is finite, e.g. X, and the second one not, then the elements of set X may be added at the beginning of the sequence determined by the set Y. This sequence includes all elements of both sets. Hence  X ∪ Y is an enumerable set.

Ad 2. Let us take the indexed family X = (X_i)_{i ∈N} and let every set X_i of it be enumerable. In order to simplify our reasoning assume that the sets of this family are pairwise disjoint (try to study other cases using lemma 9.2.2). It follows that every set of the family can be represented as some infinite sequence:

X_i = (x_i0, x_i1, x_i2, x_i3, x_i4, ...) for i ∈N.

If we number first the elements for which sum of indexes is equal to 0, then those elements, for which the sum of indexes is equal to 1 etc., see Figure 9.2.3(a), then we obtain the following sequence:

x₀₀, x₀₁, x₁₀, x₀₂, x₁₁, x₂₀, x₀₃, x₁₂, x₂₁, x₃₀, ...

which stores all elements of every family's set. Therefore, the generalized union  ⎩ ⎭ _{i ∈N} X_i is an enumerable set. ♦

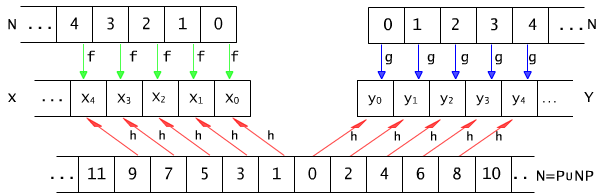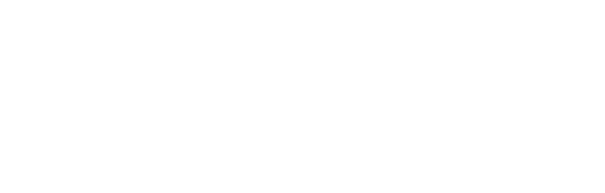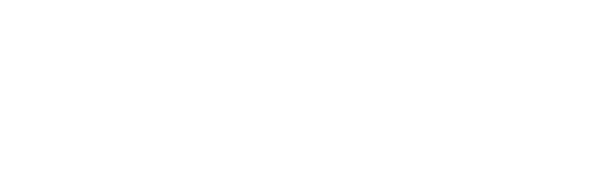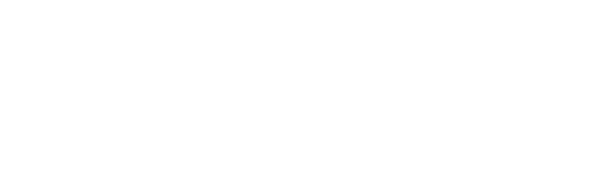
Fig. 9.2.2 the set-theoretical union of infinite countable sets is an  infinite countable set.

Proof.

Let X and Y be infinite countable sets as well as f and g be functions which state equipotence of these sets with the set of natural numbers, f : N → X i g : N → Y. Denote f(i) = x_i, g(i) = y_i,

X = (x_i)_{i ∈N} and Y = (y_i) _{i ∈N}.

Now, we construct an infinite array which corresponds to the product X × Y as it is presented on Fig. 9.2.3(b). The j-th position  (i.e. j-th column) in the i-th row corresponds to the pair (x_i, y_j). Our next step is to line up the array's elements in a sequence.  In order to do this one can use the so-called diagonal method. See Fig. 9.2.3(b) to understand the elements' numbering order. ♦

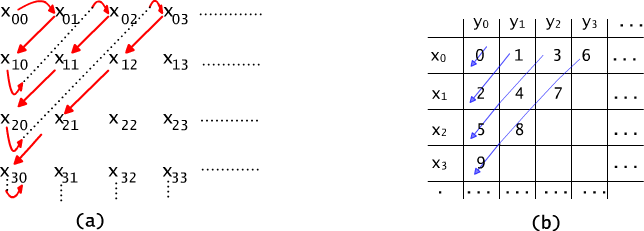
Fig. 9.2.3 (a) Successive rows of an infinite array store elements of set X₀ = (x_0i)_{i ∈N}, X₁ =(x_1i)_{i ∈N} etc. The line marked with arrows describes the ordering of the elements of generalized set-theoretical union of the sets (X_i)_{i ∈N}. (b) Successive rows and columns of the infinite array are numbered respectively with elements of the sets X = (x_i)_{i ∈N} and Y = (y_i)_{i ∈N}. The marked line suggests the order of numbering of the Cartesian product X × Y elements.

Conclusion. The set of all rational numbers  Q is  countable.

Question 9.2.2 Is the Cartesian product of any finite family of countable sets also a countable set?

Problem 9.2.1 Prove that the set of all words over a finite alphabet is a finite set.

Solution.

Let Σ stand for an arbitrary finite, non-empty alphabet. The set of words over this alphabet Σ* is, as we already know (see subsection 1.6), a generalized union of sets {λ}, Σ, Σ², Σ³ ... . Because each of these sets is finite and, therefore, at most countable, then, according to lemma 9.2.3, the set Σ* is also an at most countable set.  To see that Σ* is infinite, note, that it contains the infinite sequence of words a, aa, aaa, aaaa,...  for any  a form Σ.

« previous section

next section »