Before we start to solve new problems, we introduce a few applications of ideas and formulas just presented (see section 11). In order to do that, let us remind ourselves of the we following facts:

1. if there exists a one-to-one function from one set to another, then they are equipotent (see lecture 9),
2. the number of k-element subsets of an n-element set is described with the Newton's symbol .

Example 12.1.1

How many different natural numbers less than 2ⁿ exist such that their binary system representation includes exactly k ones?
Solution. Every natural number less than 2ⁿ uses in binary representation at most n symbols. However, every n-element sequence a_n-1, ...,  a₁ ,a₀ over the alphabet {0,1} can be treated as a characteristic function of some set A_n, A_n ⊆ {0, 1, 2..., n-1}, namely:

i ∈ A_n if and only if a_i = 1.

Set A_n stores information about the positions of ones  in the sequence a_n-1, ...,  a₁ ,a₀ (e.g. for n=7 we have 75 = (1001011)₂ , hence the corresponding set A₇ = {6,3,1,0}). A mapping which any arbitrary natural number n  assigns to the set A_n  is an one-to-one function. A set A_n has the cardinality k if and only if  n has exactly k ones in its binary representation. Thus, a number of binary sequences (of the length n) which includes k ones is equal to a number of sets A_n such that |A_n| = k, and is equal to the number of all k-element subsets of the set {0, 1, 2, ..., n-1}. According to theorem 11.5.1, there are such sets.

Example 12.1.2

Let G be an n-vertex, undirected complete graph (i.e. every graph's vertex has an undirected edge to any other) without loops (i.e. there is no edge which starts and ends in the same vertex). How many edges are there in this graph?

Solution. Each edge of the graph G  is unambiguously defined by two different vertices (no loops): starting vertex, ending vertex, therefore we deal with a 2-element set. Because by problem's assumptions G is undirected, thus  (x,y) as well as (y,x) describes the same edge. Hence, the number of edges is equal to a number of different 2-element subsets in an n-element set that is .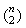
Notice, that the result in the example 12.1.2 can be derived via another way of reasoning. We know that |X × Y| = |X| * |Y|. Because, the considered above graph has n vertices, thus a number of ordered vertices' pairs amounts to n². Again, we do not count loop edges, as a result, there are only n² - n non-looped edges. Moreover, this number must be divided by 2, since the graph is undirected.  Hence, the final result (n²-n)/2  is exactly equal to the previous answer  .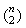

Example 12.1.3

Solution. Notice, that now we are interested only in n-length paths. Furthermore, two arbitrary ways are different only within the scope of vertex order. Thus, there exists a mutually unambiguous assignment between the set of paths and the set of permutations over {1,2, ...,n}. Using this fact, we can conclude that in an undirected complete n-vertex graph there are exactly n! Hamiltonian paths.

Question 12.1.1 Is there an undirected graph with no Hamilton's path?

Example 12.1.4

Consider a set of 5 cards taken from a standard deck of playing cards. We say that such a set is of type (x,y) if it consists of three cards of type x (the cards differ only in colours) and two cards of type y and x is different than y. For example (5,5,5,8,8) is a 5-element set of type (5,8).

(a) How many 5-element sets of type (7,D) exist?

(b) How many different 5-element set's types exist?

Solution. (a) We choose 3 cards of 7-type from a set of 4 possible (as there are only 4 cards of the same type) and 2 cards of D-type from a set of 4 occurring in a card deck. Therefore, we get 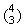potential choices of 7-kind cards as well as 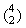potential choices of D-kind cards.  We have 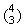* 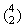sets together, i.e. there are 24 different 5-element sets of type (7,D).

Solution. (b) To fix a number of different types of 5-element  sets, we need to choose type x from 13 possible types and after that we choose type y from 12 remaining. Thus we can build 13*12 different pairs (x,y).

Question 12.1.2 How many different 5-element sets of any type (x,y)   exist?

Example 12.1.5

Some shop offers 3 kinds of ice-creams (yoghurt, coffee, vanilla) sold in 5-scoop cornets. How many different ice-desserts may be composed if we do not care about an order of ice scoops in a cornet?

Solution. Every ice-dessert consists of some number of yoghurt, coffee as well as vanilla scoops, denoted respectively with y, c and v letters. We know that y ≤ 5, c ≤ 5, v ≤ 5 and y+c+v = 5. It is easy to encode every ice-dessert on 7 blanks so that two of them must be checked. Checked positions separate groups of not checked blanks which correspond with ice scoops of the same kind (see fig. 12.1). In order to calculate the number of different ice-desserts we need to find out in how many different ways we can check two blanks from 7 possible positions. Of course this quantity is equal to the number of different 2-element subsets over 7-element set, i.e. 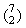 , therefore the answer is 21.

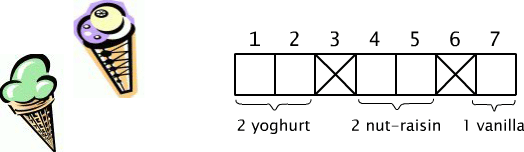
Fig. 12.1.1 A way of encoding ice-dessert.

At the end of this subsection we want to say a few words about the binomial coefficient name's origin. Thus in the XVII century Isaac Newton found a general expending notation form of a binomial (x+y) n-th power.

The equation included in the theorem 12.1.1 is usually called the Newton's binominal. Coefficients from the right side of this equation are Newton's binominal coefficients.

Notice, that every element of considered sum which arises after n-time multiplication

(x+y) ⋅ (x+y) ⋅ ... ⋅ (x+y)

has the following form: (xⁱ ⋅ y^j) and i+j = n, i.e. from i coefficients of this product we choose x and from remaining we choose y. If for arbitrary i we consider xⁱ y ^n-i coefficients then a number of them is equal to a number of drawing i elements form n-element set i.e. (n over i). Because i can take a value form 0 to n thus, we derive a right side of Newton's equation.

Now a complete proof for theorem 12.1.1 can be made by an induction on n. We leave it as a task for you.