We want to devote this subsection to the problem of counting different binary relations over some finite set.

Let X be an n-element set. Firstly we ask: "How many different binary relations can be established in this set?". Every binary relation over X is a subset of a Cartesian product X × X. It follows that a number of binary relations is equal to a number of different subsets of product set X × X. Because product X × X has exactly n² elements thus, according to the power set's theorem (see lecture 9) there are 2 ^n*n binary relations in X.

Every binary relation defined over a finite set may be presented (described) as a square matrix which columns and rows are marked with set's elements (adjacency matrix, see subsection 2.2). We put 1 in the position (x,y) of the matrix when the pair (x,y) belongs to the relation.  Thus, our above-mentioned task is equivalent to the method of counting  by putting 1 in the n × n-element matrix. But we already know the answer.

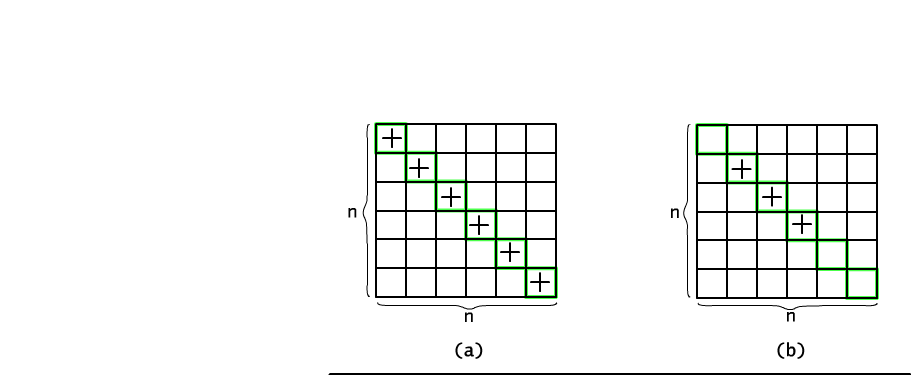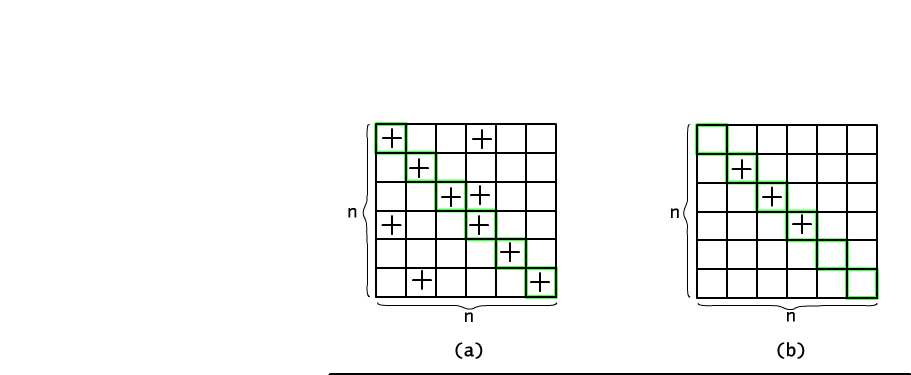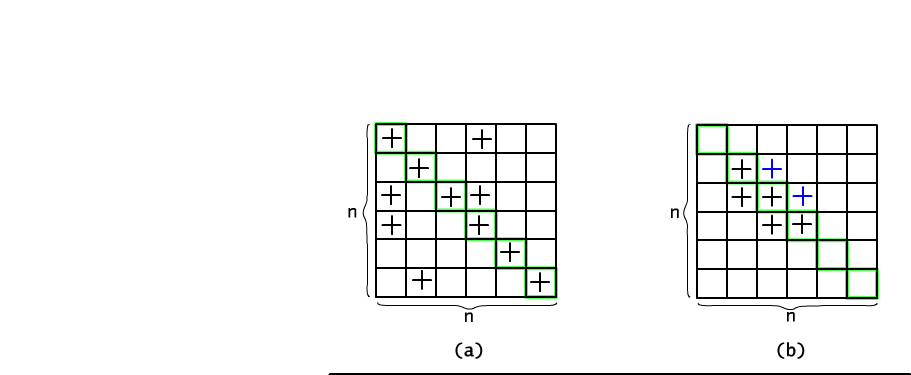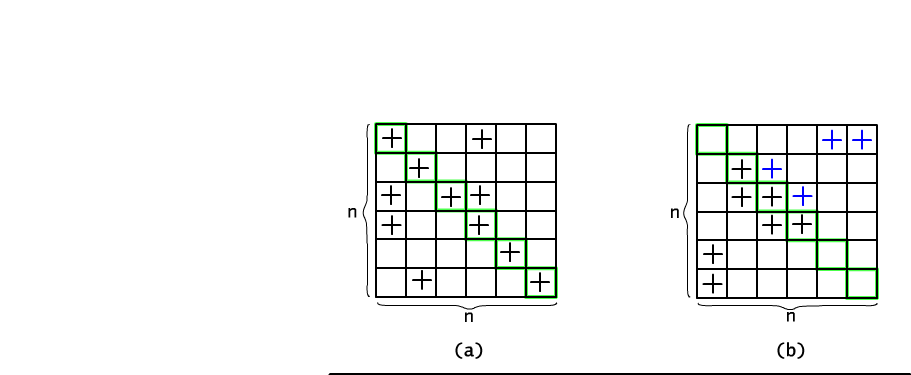
Now we make some restrictions on binary relations' type. Assume that we want to count only reflexive relations. The adjacency matrix of reflexive relation has a very characteristic form: all diagonal places are filled up with 1 (see Fig. 12.2.1). Of course, non-diagonal places may or may not be filled up. Therefore, to create a reflexive relation we need to fill up all diagonal and any subset of remaining (n²-n) positions with the symbol 1. The correspondence between reflexive relations and sets  of filled up positions is mutually unambiguous. Using this fact we may estimate a number of reflexive relations as a number of subsets over (n²-n)-element set. So, the answer is  2^(n-1)n.

Fig. 12.2.1 Counting  reflexive (a)  and symmetric (b) relations.

In a similar way we may count all symmetric relations. In order to define a symmetric relation it is enough to freely fill up a triangular part of adjacency matrix (including diagonal) and after that reflect this part to the unfilled one (i.e. if we mark position (x,y) then after reflection position (y,x) should be also marked). Because the initial selection concerns only n(n+1)/2 pairs (triangular matrix with diagonal), thus there are exactly 2^(n+1)n/2 different symmetric relations.

Question 12.2.1 How many reflexive and symmetric relations may be established over an n-element set?

Question 12.2.2 How many different linear orderings can be defined in an n-element set?

« previous section

« next section