Jest rzeczą naturalną, że mając wiele obiektów tego samego typu chcemy je ze sobą porównywać. W zasadzie, już w tym krótkim wstępie nie ustrzegliśmy się od tego. Wprowadzimy teraz formalnie dwie relacje pozwalające porównywać zbiory.

Definicja 1.2.1 Równość zbiorów

Powiemy, że dwa zbiory X i Y są równe, X = Y, wtedy i tylko wtedy, gdy dla dowolnego x, jeśli x ∈ X, to x ∈ Y i jeśli x ∈ Y , to x ∈ X. Będziemy stosowali również nieco krótszy zapis symboliczny :

X = Y wttw (x ∈ X ⇒ x ∈ Y) oraz (x ∈ Y ⇒ x ∈ X).

W myśl tej definicji, dwa zbiory są równe, jeśli posiadają te same elementy. Oczywiście, wypisanie kilkakrotne tego samego elementu lub zapisanie elementów zbioru w innej kolejności, nie zmienia zbioru. Stąd mamy:

{x ∈ N : x² < 0 } = {x ∈ R : x = x+1} = {x: x jest pierwiastkiem rzeczywistym równania x² +2x + 2 = 0}.

Uwaga. W dalszym ciągu, wypisując elementy zbioru w postaci {x₁, ..., x_n} będziemy milcząco zakładali, że są one różne. Liczbę elementów w zbiorze {x₁,...,x_n} nazywać będziemy mocą zbioru i oznaczymy przez |{x₁,...,x_n}|, a więc |{x₁,...,x_n}|= n.

Zanotujmy prostą, ale wielokrotnie wykorzystywaną, konsekwencję przyjętej definicji:

Lemat 1.2.1

Dla dowolnych zbiorów X, Y, Z, jeśli X = Y oraz Y = Z, to X = Z.

Warto też zastanowić się przez chwilę nad zaprzeczeniem równości. Co to znaczy, że X ≠ Y? Zgodnie z przyjętą definicją równości, musi istnieć taki element zbioru X, który nie należy do Y, lub musi istnieć taki element zbioru Y, który nie jest elementem zbioru X. Na przykład, R ≠ N, bo √2 ∈ R i √2 ∉ N. Z drugiej strony jednak, każda liczba naturalna jest liczbą rzeczywistą. Zbiór liczb naturalnych zawiera się w zbiorze liczb rzeczywistych.

Definicja 1.2.2 Zawieranie zbiorów

Powiemy, że zbiór X jest zawarty w Y albo, że zbiór Y zawiera zbiór X , i piszemy X ⊆ Y wttw każdy element zbioru X jest równocześnie elementem zbioru Y.

Jeśli X ⊆ Y, to w szczególności X może być równe Y. Aby zaznaczyć, że taka sytuacja nie może mieć miejsca, piszemy X ⊂ Y. O relacji ⊆ mówimy, że jest to inkluzja albo relacja zawierania. Natomiast symbol ⊂ nazywamy zawieraniem właściwym. O zbiorze X, takim że X ⊆ Y (X ⊂ Y) mówimy, że jest podzbiorem zbioru Y (podzbiorem właściwym zbioru Y), a o Y mówimy, że jest nadzbiorem zbioru X.

Zbiory i zachodzące miedzy nimi związki, będziemy przedstawiali również graficznie w postaci obszarów (kół) na płaszczyźnie. Fakt, że zbiór A jest zawarty w zbiorze B można przedstawić na rysunku w postaci tzw. diagramu Venna, por. Rys.1.2.1.

1. Zbiór studentek PJWSTK jest oczywiście podzbiorem zbioru wszystkich osób studiujących w PJWSTK. Natomiast zbiór wszystkich studentów PJWSTK jest podzbiorem zbioru wszystkich studentów studiujących w Polsce.

2. Na szczególną uwagę zasługują pewne wyróżnione podzbiory zbioru liczb rzeczywistych zwane przedziałami. Przedziałem domkniętym o końcach a, b nazywamy zbiór [a, b] = {x ∈ R : a ≤ x ≤ b}. Przedziałem otwartym o końcach a, b nazywamy zbiór (a, b) = {x ∈ R : a < x < b}. Można mówić także o przedziałach otwarto domkniętych lub domknięto otwartych, jeśli jeden z końców przedziału do niego należy.

Zauważmy, że jeżeli nie jest prawdą, że zbiór A zawiera się w zbiorze B, to możliwe są następujące 3 przypadki (por. Rys.1.2.2):

Zauważmy, że zbiór A nie jest zawarty w B wtedy i tylko wtedy, gdy istnieje a, a ∈ A, a ∉ B.

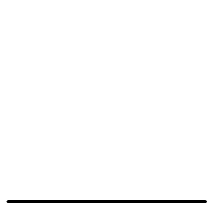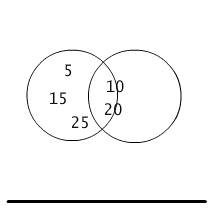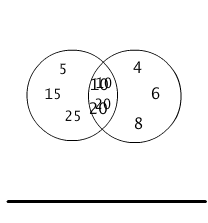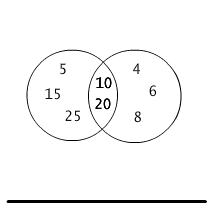
Zbiór liczb podzielnych przez 2 nie jest podzbiorem zbioru liczb podzielnych przez 5, bo np.4 jest podzielne przez 2 i nie jest podzielne przez 5. Nie jest też odwrotnie: zbiór liczb podzielnych przez 5 nie jest podzbiorem zbioru liczb podzielnych przez 2, bo np. 15 jest podzielne przez 5, a nie jest podzielne przez 2 (por. Rys.1.2.3).

Uwaga. Dla dowolnego x, jeśli x ∈ A, to {x} ⊆ A, x ∈ {x} ale x ≠ {x}. Nie należy mylić elementu x ze zbiorem jednoelementowym {x}.

Zanotujemy teraz pewne proste fakty dotyczące inkluzji (zawierania zbiorów), wynikające z przyjętych wcześniej definicji.

Twierdzenie 1.2.1

Dla dowolnych zbiorów A, B, C zachodzą następujące zależności:

∅ ⊆ A,
A ⊆ A,
Jeśli A ⊆ B i B ⊆ C, to A ⊆ C.

Zależność 1 wyraża fakt, że zbiór pusty jest podzbiorem dowolnego zbioru. Rzeczywiście, mamy pokazać, że każdy element należący do zbioru ∅, należy też do A. Ale do zbioru pustego nie należy żaden element. Zatem zachodzi ∅ ⊆ A.
Zależność 2 jest oczywista, na mocy definicji zawierania.
Zależność 3 jest zwana prawem przechodniości dla relacji inkluzji. Aby wykazać jej słuszność, załóżmy, że A ⊆ B i B ⊆ C. Jeśli jakiś element a należy do zbioru A, to na mocy pierwszego założenia a ∈ B, a z drugiego a ∈ C. Zatem, jeśli tylko a ∈ A, to a ∈ C. ♦

Pytanie 1.2.2: Jak zapisać krótko, że A nie zawiera się w B lub B nie zawiera się w A?

Definicja 1.2.3

Zbiorem potęgowym nazywamy zbiór P(A) złożony z wszystkich podzbiorów zbioru A. Zbiór potęgowy oznaczamy też czasem przez 2^A.

(a) Niech A = {0, 1} wtedy zbiór wszystkich jego podzbiorów, P(A), składa się z 4 zbiorów ∅, {0}, {1}, {0,1}. Zatem P(A) = { ∅, {0},{1}, {0,1}}.

(b) Jeśli B = {1, {2}, {1,2}}, to jego elementami są: liczba 1, zbiór jednoelementowy {2} oraz zbiór dwuelementowy {1,2}. Podzbiorami zbioru B są natomiast: zbiór pusty, podzbiory jednoelementowe {1}, {{2}}, {{1,2}}, podzbiory dwuelementowe {1, {2}}, {1, {1,2}}, {{2}, {1,2}} oraz jeden podzbiór trzyelementowy {1, {2}, {1,2}} identyczny z B. Zatem P(B) ma 8 elementów.

Uwaga. P(A) nigdy nie jest zbiorem pustym. Nawet, gdy A jest zbiorem pustym, to P(A) jest zbiorem jedno-elementowym, bo chociaż A nie posiada elementów, to ma jeden podzbiór ∅. Czyli P( ∅ ) = { ∅ }.

Pytanie 1.2.3: Ile elementów ma zbiór P(X), jeśli zbiór X ma 4 elementy?