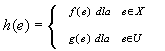
| « poprzedni punkt | następny punkt » |
Funkcje są szczególnym przypadkiem relacji, zatem operacje określone na relacjach mogą być wykonywane również na funkcjach. Niestety nie wszystkie prowadzą od funkcji do funkcji.
Rozważmy na początek sumę teoriomnogościową dwóch funkcji f i g, f: X → Y i g: U → V.
f ∪ g = { (x,y) : y = f(x) } ∪ {(u,v) : v = g(u)}
O ile zbiory X i U są rozłączne, to suma f ∪ g jest funkcją, ponieważ nie ma dwóch par, które miałyby identyczne poprzedniki i różne następniki. Suma f ∪ g determinuje w tym przypadku funkcję h zdefiniowaną warunkowo
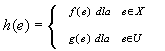
W przeciwnym przypadku, gdy X ∩ U ≠ ∅, suma f ∪ g nie musi być funkcją, por. Rys. 4.3.1. Jeśli x ∈ X i x ∈ U, ale f(x) ≠ g(x), to do zbioru f ∪ g należą obie pary (x,f(x)) i (x,g(x)), a więc nie jest to funkcja.
Rys. 4.3.1 Suma funkcji może, ale nie musi być funkcją.
W przypadku przecięcia funkcji, f ∩ g, sprawa jest o wiele prostsza:
f ∩ g = { (x,y) : y = f(x)} ∩ {(u,v) : v = g(u)}
jest funkcją odwzorowującą X ∩ U w Y ∩ V.
Pytanie 4.3.1: Dana jest funkcja całkowita f : X → X. Kiedy uzupełnienie zbioru {(x,f(x))}x ∈ X w produkcie X × X jest funkcją?
Załóżmy teraz, że ograniczymy się do funkcji o wartościach rzeczywistych, czyli rozważamy funkcje f : X → R (zbiór X niekoniecznie musi być zbiorem liczb rzeczywistych). Na takich funkcjach możemy wykonywać operacje arytmetyczne tworząc w ten sposób nowe funkcje. Niech f1 : X → R i f2 : X → R, wtedy możemy utworzyć funkcje f, g, h następująco:
f(x) = f1(x) + f2(x),
g(x) = f1(x) * f2(x),
h(x) = f1(x) / f2(x).
Zauważmy, że o ile funkcje f i g są określone dla wszystkich tych x, dla których określone są funkcje f1 i f2 (czyli dla x ∈ Dom(f1) ∩ Dom(f2) ), to funkcja h jest określona jedynie dla x ∈ Dom(f1) ∩ Dom(f2) ∩ {x : f2 (x) ≠ 0}.
Pytanie 4.3.2: Czy suma dowolnych funkcji różnowartościowych f1 : R → R i f2 : R → R określona wzorem (f1 + f2 )(x) = f1(x) + f2(x), jest zawsze funkcją różnowartościową?
----- Sprawdź odpowiedź -----Zajmiemy się teraz operacjami składania i odwracania funkcji. Niech f: X → Y i g: Y → V. Na mocy definicji 2.4.2, f ° g jest relacją określoną w produkcie X × V. Gdyby dla pewnych różnych elementów v' i v" ze zbioru V,
(x,v') ∈ f ° g, (x,v") ∈ f ° g
wówczas istniałyby elementy y' i y" w zbiorze Y, takie że
x f y' i y' g v' oraz x f y" i y" g v".
Ponieważ relacja f jest funkcją, zatem y ' = y". Wtedy jednak mamy y' g v' i y' g v", co przeczy założeniu, że g też jest funkcją. Z tego rozumowania wynika, że o ile relacje biorące udział w złożeniu są funkcjami, to ich złożenie też jest funkcją (por. Rys. 4.3.2). Pozwala to przyjąć następującą definicję składania.
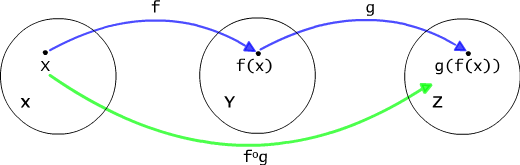
Rys. 4.3.2 Złożenie funkcji.
Definicja 4.3.1
Jeżeli f: X → Y i g: Y → V, to złożeniem funkcji f i g nazywamy funkcję f ° g : X → V, określoną wzorem
(f ° g)(x) = g(f(x)) dla wszystkich x takich, że x ∈ Dom(f) i f(x) ∈ Dom(g).
Oczywiście wynika stąd natychmiast, że złożenie funkcji całkowitych jest funkcją całkowitą.
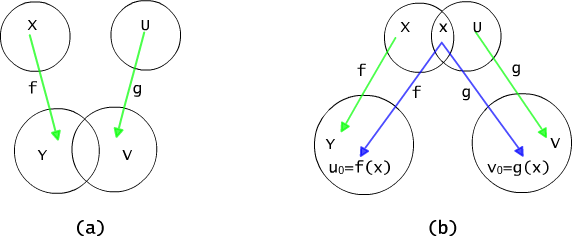
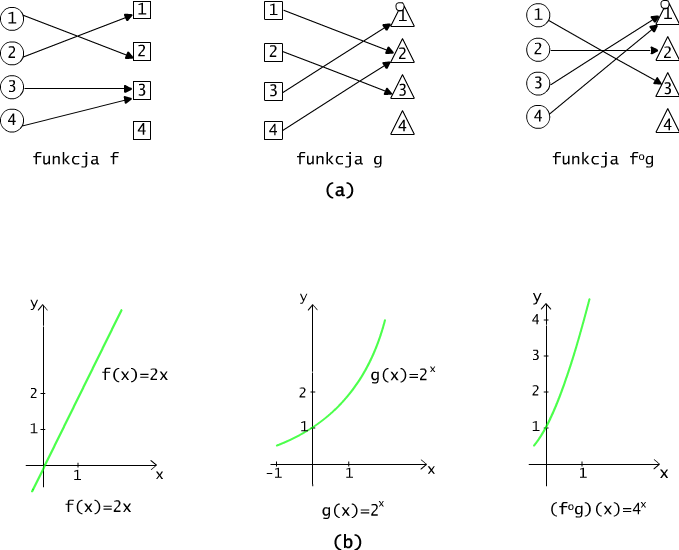
Na rysunku 4.3.3 przedstawiono przykłady funkcji i ich złożeń. Złożeniem funkcji f(x) = x2 +1 z funkcją g(x) = x+5, określonych na zbiorze liczb rzeczywistych i o wartościach rzeczywistych, jest funkcja h : R → R taka, że
h(x) = (f ° g)(x) = g(f(x)) = g(x2 +1) = (x2 +1) +5 = x2 +6
Złożeniem funkcji g(x) = x+5 z funkcją f(x) = x2 +1, jest funkcją h' : R → R taką, że
h'(x) = (g ° f)(x) = f(g(x)) = f(x +5) = ((x+5)2 +1) = x2 +10x +26
Rys. 4.3.3 (a),(b) Przykłady funkcji i ich złożeń.
Zanotujmy obserwację wynikającą z omawianych wyżej przykładów:
Lemat 4.3.1
Równość występującą w tezie (2) należy rozumieć następująco: lewa strona równości jest określona wtedy i tylko wtedy, gdy prawa strona równości jest określona i o ile obie strony mają określone wartości, to są one równe.
Dowód (1) wynika wprost z przykładu omówionego powyżej. Dla dowodu (2) zauważmy, że przy założeniach o określoności, dla dowolnego x, mamy
f ° (g ° h)(x) = (g ° h) (f(x)) = h(g(f(x))) = h((f ° g )(x)). = ((f ° g ) ° h)(x).
Pytanie 4.3.2: Czy złożenie dwóch permutacji jest permutacją ?
Lemat 4.3.2
Niech f: X → Y i g: Y → Z.
Dowód.
Ad. (1) Niech f i g będą funkcjami różnowartościowymi i niech x1 ≠ x2 . Ponieważ f jest z założenia funkcją 1-1, więc f(x1) ≠ f(x2). Funkcja g też jest 1-1, zatem g(f(x1)) ≠ g(f(x2)), a stąd g(f(x1)) ≠ g( f(x2)), czyli (f ° g) jest funkcją różnowartościową.
Ad. (2) Weźmy dowolny element z0 ∈ Z. Chcemy pokazać, że istnieje dla tego elementu taki argument x0, że (f ° g)(x0) = z0. Rzeczywiście, skoro g jest odwzorowaniem na Z, to istnieje element y0 w zbiorze Y, który jest przekształcany w z0. Podobnie funkcja f, jako odwzorowanie na zbiór Y, ma taki element x0, że f(x0) = y0 . Ostatecznie (f ° g)(x0) = g(y0 )= z0.
Definicja 4.3.2
Funkcję g: Y → X. nazywamy odwrotną do f : X → Y, jeżeli Dom(g) = Im(f) i Dom(f) =Im(G) oraz g(f(x))= x dla wszystkich x ∈ Dom(f).

Rys. 4.3.4 Relacja odwrotna do funkcji nie musi być funkcją.
Przykład 4.3.1
(1) Na rysunku 4.3.4 przedstawiliśmy dwie relacje r1 i r2 i relacje do nich odwrotne r1-1, r2-1. Zauważmy, że w pierwszym przypadku obie relacje r1 i r1-1 są funkcjami. W drugim przypadku, chociaż relacja r2 jest funkcją, to relacja odwrotna r2-1 nie jest funkcją, bo obie pary (4,2) i (4, -2) należą do r2-1. Na czym to polega? Otóż, relacja r1 jest funkcją różnowartościową, a r2 nie.
(2) Rozważmy jako jeszcze jeden przykład funkcję f : N → NP, f(n) = 2n+1 odwzorowującą zbiór liczb naturalnych w zbiór liczb nieparzystych NP. Funkcja g : NP → N określona wzorem g(n) = (n-1) div 2 dla n ∈ N, jest funkcją odwrotną do f. Rzeczywiście g(f(n)) = g(2n+1) = (2n+1 -1) div 2 = 2n div 2 = n.
(3) Funkcja wykładnicza f(x) = 2x ma funkcję odwrotną zwaną logarytmem przy podstawie 2, oznaczanym zwykle przez lg, lg : R+ → R ,
lg x = a wttw 2 a = x.
Funkcję odwrotną do danej funkcji różnowartościowej f oznaczamy, podobnie jak relację odwrotną, przez f -1.
Uwaga Dla każdej funkcji różnowartościowej odwzorowującej X na Y istnieje dokładnie jedna funkcja odwrotna. Funkcja odwrotna do danej funkcji różnowartościowej też jest różnowartościowa.
Pytanie 4.3.3: Niech będzie relacją w zbiorze wszystkich funkcji ze zbioru X w zbiór X taką, że f ∼ g wttw f jest funkcją odwrotną do g. Czy ta relacja jest symetryczna?
Lemat 4.3.3
Dla dowolnych funkcji f : X → Y i g : Y → Z, jeżeli f i g są wzajemnie jednoznaczne (są bijekcjami), to istnieją funkcje (f ° g) -1 : Z → X, g -1 : Z → Y, f -1 : Y → X oraz zachodzi równość (f ° g) -1 = g -1 ° f -1.
Dowód
Na mocy założenia i lematu 4.3.2, złożenie (f ° g) jest funkcją różnowartościową odwzorowującą X na Z. Zatem istnieje funkcja odwrotna (f ° g) -1, która odwzorowuje Z na X. Dla dowolnych z ∈ Z i x ∈ X mamy
(f ° g) -1(z) = x wttw (f ° g)(x) = z wttw g(f(x)) = z wttw istnieje takie y, że y = f(x) i g(y) = z wttw istnieje takie y, że f -1 (y) = x oraz g-1 (z) =y wttw f -1 (g-1(z)) = x wttw (g -1 ° f -1)(z) = x.
| « poprzedni punkt | następny punkt » |