W zbiorze częściowo uporządkowanym <X, ≤ > wyróżnimy pewne elementy ze względu na przyjęty porządek. Jeśli grupa osób ustawiła się w kolejkę przed okienkiem w banku, to kolejka ta wyznacza porządek obsługiwania tych osób. W tej grupie osoba pierwsza w kolejce jest w pewnym sensie wyróżniona, bo zostanie obsłużona jako pierwsza. Osoba stojąca na końcu kolejki, wyróżnia się tym, że będzie obsłużona jako ostatnia.

Definicja 6.3.1

Element x₀ nazywamy maksymalnym w zbiorze uporządkowanym <X, ≤ > wtedy i tylko wtedy, gdy nie istnieje y ∈ X, takie że x₀ ≠ y i x₀ ≤ y.

Element x₀ nazywamy minimalnym w zbiorze uporządkowanym <X, ≤ > wtedy i tylko wtedy, gdy nie istnieje y ∈ X takie, że x₀ ≠ y i y ≤ x₀ .

W diagramie Hassego relacji porządku, elementy minimalne i maksymalne bardzo łatwo zauważyć: te pierwsze są na dole, a te drugie na górze diagramu, por. Rys. 6.3.1.

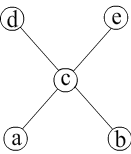
Rys. 6.3.1 Diagram Hssego pewnej relacji częściowego porządku w zbiorze {a, b, c, d, e}. Elementy a, b są elementami minimalnymi, a elementy d, e maksymalnymi w tym porządku.

Pytanie 6.3.1: Czy w zbiorze liczb naturalnych z porządkiem ≤ można wskazać elementy minimalne lub maksymalne?

Definicja 6.3.2

Element x₀ nazywamy najmniejszym w zbiorze uporządkowanym <X, ≤ > wtedy i tylko wtedy, gdy dla każdego y ∈ X, x₀ ≤ y.

Element x₀ nazywamy największym w zbiorze uporządkowanym <X, ≤ > wtedy i tylko wtedy, gdy dla wszystkich y ∈ X i y ≤ x₀ .

Zwróćmy uwagę na subtelną różnicę w definicjach elementów najmniejszego i minimalnego oraz elementów największego i maksymalnego.

Oczywiście, element najmniejszy (największy) jest też elementem minimalnym (maksymalnym). Nie jest jednak odwrotnie, jak pokażą przykłady.

(1) W zbiorze liczb rzeczywistych uporządkowanych przez relację ≤ nie ma elementów minimalnych i nie ma elementów maksymalnych. Zbiór R jest nieskończony i dla każdej liczby rzeczywistej istnieje zarówno od niej większa liczba rzeczywista jak i istnieje liczba od niej mniejsza. Z tego też powodu, nie ma w tym zbiorze ani elementu najmniejszego ani największego.

(2) W zbiorze podzbiorów zbioru X = {R, G, B} uporządkowanym przez relację inkluzji (por. przykład 6.2.1(1)) istnieje element maksymalny {R, G, B} i element minimalny ∅. Zbiory te są jednocześnie elementem największym i najmniejszym w P(X). Jeśli rozważymy zbiór P(X) \{ ∅ } (tzn. zbiór wszystkich niepustych podzbiorów X) z inkluzją jako porządkiem, to teraz mamy aż trzy elementy minimalne {R}, {G}, {B}, natomiast nie ma w tym zbiorze elementu najmniejszego.

(3) W zbiorze {1, 2, ..., 9} uporządkowanym przez relację podzielności | (por. Rys. 6.2.2(a)) istnieje jeden element minimalny, który jest jednocześnie elementem najmniejszym, i istnieje pięć elementów maksymalnych: 5, 6, 7, 8, 9. Nie ma w tym zbiorze elementu największego.

Jak wynika z przedstawionych przykładów, w zbiorze uporządkowanym może być więcej niż jeden element minimalny, więcej niż jeden element maksymalny, ale co najwyżej jeden element najmniejszy i co najwyżej jeden element największy.

Pytanie 6.3.2: Czy można podać przykład zbioru, który ma tylko jeden element maksymalny i nie posiada elementu największego?

Udowodnić, że w każdym zbiorze uporządkowanym istnieje co najwyżej jeden element największy.

Rozwiązanie: Gdyby w pewnym zbiorze uporządkowanym przez pewną relację ≤ istniały dwa elementy największe a i b, to dla każdego elementu x tego zbioru byłoby: x ≤ a i x ≤ b. W szczególności biorąc za x raz a, a drugi raz b otrzymamy b ≤ a i a ≤ b. Ponieważ relacja porządku jest antysymetryczna, więc musi być a=b.