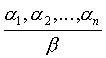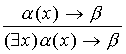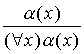8.6. Reguły wnioskowania
Definicja 8.6.1
Reguły dowodzenia (inaczej reguły wnioskowania) są przekształceniami
postaci
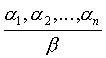
które pewnemu skończonemu zbiorowi formuł (formuł) α1,
..., αn,
przyporządkowują formułę β, w
taki sposób, że dla dowolnej struktury danych STR takiej,
że STR |= α1
∧... ∧
αn,
mamy STR |= β.
Formuły α1,
..., αn
są nazywane przesłankami reguły, a formuła β jest nazywana wnioskiem.
Podobnie jak w rachunku zdań, w rachunku predykatów, jedną z
podstawowych reguł dowodzenia jest reguła modus ponens. Innymi
przykładami reguł często stosowanych w dowodach matematycznych są:
reguła uogólniania (generalizacji) i reguła dołączania kwantyfikatora
egzystencjalnego, które przedstawiamy poniżej.
Lemat 8.6.1
Dla dowolnej formuły α(x) i dowolnej
formuły β, w której zmienna
x nie występuje,
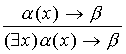
jest poprawną regułą dowodzenia.
Dowód.
Przypuśćmy przeciwnie, że
(1) STR|= ( α(x) →
β
) oraz
(2) nie zachodzi STR|= (( ∃x)α(x) → β).
Wtedy z (2) dla pewnego wartościowania v mamy STR,v|= ( ∃x) α(x) i STR,v|= ¬β. Stąd na mocy
definicji semantyki kwantyfikatorów, dla pewnego a ∈
STR,
STR,v(x/a)|= α(x)
STR,v(x/a)|= ¬ β
(ponieważ wartość zmiennej x nie ma wpływu na wartość formuły β).
W konsekwencji STR,v(x/a)|= ¬
( α(x) → β). Sprzeczność z (1).
Wykazaliśmy tym samym, że z prawdziwości formuły postaci ( α(x) → β
) wynika prawdziwość formuły (( ∃ x) α(x) → β).
Lemat 8.6.2
Dla dowolnej formuły α(x),
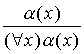
jest
poprawną regułą dowodzenia (reguła uogólniania).
Dowód.
Skoro STR|= α(x) ,
to niezależnie od wartości zmiennej x, tzn. przy każdym wartościowaniu
mamy STR,v(a/x) |= α(x).
Stąd oczywiście STR, v|= ( ∀x)
α(x) dla każdego v, czyli ostatecznie STR|= ( ∀x)
α(x).
Zauważmy, że jeśli przesłanki poprawnej reguły dowodzenia są
tautologiami, to wniosek w tej regule jest też tautologią. Zatem, ze
znanych już nam praw rachunku predykatów, za pomocą poprawnych reguł
dowodzenia, możemy uzyskać nowe interesujące prawa rachunku predykatów.
Zastosowanie tautologii i reguł rachunku predykatów do dowodzenia
przedstawimy w następującym przykładzie.
Przykład 8.6.1
Niech (Ai)i ∈
I będzie rodziną podzbiorów zbioru X oraz niech f będzie funkcją
f : X → Y. Udowodnimy, że
f( ⎧⎫i ∈ I Ai) ⊆ ⎧⎫i ∈
I f(Ai).
Dowód:
1. y ∈ f( ⎧⎫i ∈
I Ai) na mocy def. obrazu funkcji
2. ( ∃ x ∈
X)( x ∈ ìüi ∈
I Ai ∧ f(x)=y) z definicji
iloczynu uogólnionego
3. ( ∃ x ∈
X) (( ∀ i ∈
I) x ∈
Ai ∧ f(x)=y) z prawa
włączania-wyłączania
4. ( ∃ x ∈
X) ( ∀ i ∈
I) (x ∈
Ai ∧ f(x)=y) częściowa
przemienność kwantyfikatorów
5.( ∀ i ∈I) ( ∃ x ∈
X)(x ∈
Ai ∧ f(x)=y) z definicji
obrazu funkcji
6. ( ∀i ∈
I) y ∈ f(Ai) z definicji
iloczynu uogólnionego
7. y ∈ ⎧⎫i ∈I
f(Ai)
Niech STR będzie ustaloną strukturą danych, w której interpretujemy
rozważane formuły. Będziemy pisali krótko α
=> β dla
oznaczenia, że z prawdziwości formuły α w strukturze STR wynika prawdziwość formuły β w STR. Podobnie, będziemy
pisali α <=> β dla oznaczenia, że formuła α
jest semantycznie równoważna formule β w
strukturze STR, tzn. z prawdziwości formuły α
w STR wynika prawdziwość formuły β
w STR i odwrotnie.
Stosując tę notację w poprzednim przykładzie możemy zapisać
przedstawiony dowód w postaci: 1 <=> 2 <=> 3 <=> 4 => 5 <=> 6 <=> 7.
Czyli 1 => 7.
Przykład 8.6.2
Rozważmy następujące twierdzenie: W każdym zbiorze liniowo
uporządkowanym <X, ≤ >, jeśli x jest
elementem maksymalnym, to jest też elementem największym (por. wykład
VI).
Niech x0 będzie elementem maksymalnym w zbiorze X. Wtedy
:
¬
( ∃x) (x0 ≤
x ∧ x ≠ x0)
<=>
(na mocy praw de Morgana dla kwantyfikatorów) ( ∀x)
¬ (x0 ≤
x ∧ x ≠ x0)
<=> (na mocy praw de Morgana dla koniunkcji) ( ∀x) ( ¬ x0
≤ x ∨ ¬ x ≠ x0)
=> (ponieważ porządek ≤
jest z założenia liniowy) ( ∀x) x
≤ x0.
W informatyce również jesteśmy zmuszeni do przeprowadzania dowodów.
Napisanie programu na ogół nie wystarcza, trzeba dostarczyć argumentów,
że program rzeczywiście rozwiązuje postawione zadanie.
Przykład 8.6.3
Niech zadanie polega na obliczeniu xn, gdzie n jest
liczbą naturalną, a x liczbą rzeczywistą. Przypuśćmy, że jako
rozwiązanie problemu zaproponowano nam następujący program, gdzie
odd(m) oznacza, że m jest liczbą naturalną nieparzystą.
{ z:= x; y :=1; m := n;
while (m > 0) {
if odd(m) { y := y * z; }
m := m div 2;
z := z * z;
}
}
Czy jest to poprawne rozwiązanie postawionego zadania?
Udowodnimy, że o ile początkową wartością zmiennej n jest liczba
naturalna, to po wykonaniu programu wartością zmiennej y jest n-ta
potęga x.
Niezależnie od tego, jakie jest wartościowanie zmiennych przed
wykonaniem programu, po pierwszych instrukcjach przypisania prawdziwa
jest koniunkcja (x =z ∧ m=n ∧ y=1). Zatem przy pierwszym wejściu do pętli
"while" prawdziwa jest formuła zm * y = xn.
Przypuśćmy, że formuła ta jest prawdziwa przy i-tym wejściu do pętli
"while".
Ponieważ w zbiorze liczb rzeczywistych prawdziwe są formuły:
( ∀m ∈N)(Odd(m) ∨ ¬ Odd(m)),
( ∀m ∈N)(Odd(m) → m=2*(m div2) + 1),
( ∀m ∈N)( ¬
Odd(m) → m = 2*(m div2) )
zatem przy i-tym wejściu do pętli "while" prawdziwa jest również
formuła
Odd(m) ∧ (z * z)m div 2
* (y * z) = xn ∨
¬
Odd(m) ∧ (z * z)m div 2
* y = xn
Jeśli wartościowanie, jakie mamy aktualnie przed wykonaniem
instrukcji "if", spełnia formułę Odd(m), to program wykonuje instrukcję
{y := y * z;} zmieniającą wartość zmiennej y. W konsekwencji, po
wykonaniu instrukcji "if" (niezależnie od tego jaki był wynik testu
Odd(m) ) spełniona jest formuła (z * z)mdiv 2 *
y = xn. W wyniku zmiany wartości zmiennych przez instrukcje
{ m := m div 2; z := z * z;} otrzymujemy wartościowanie, które spełnia
formułę zm * y = xn. Zatem przy
(i+1)-szym wejściu do pętli "while" znów spełniony jest warunek zm
* y = xn. Wynika stąd, że niezależnie od tego ile
iteracji wykona nasz program, zawsze, tuż przed sprawdzeniem warunku
pętli, spełniona jest formuła zm * y = xn.
Ponieważ przy każdej iteracji pętli, zmienna m jest dzielona przez
2, zatem po skończonej liczbie iteracji wartością zmiennej m będzie 0
(zasada dobrego ufundowania zbioru liczb naturalnych, por. wykład VI).
W takim przypadku opuszczamy pętlę i kończymy obliczenia mając
spełniony warunek (m = 0 ∧ zm *
y = xn) czyli y = xn.
Wniosek : dla dowolnych x ∈ R i n ∈ N, po wykonaniu programu y = xn.