Zanim przejdziemy do rozwiązywania nowych problemów, przedstawimy kilka zastosowań poznanych wcześniej pojęć i wzorów. W przykładach, przedstawionych w tym punkcie wykładu, będziemy korzystali głównie w dwóch faktów:

1. jeśli istnieje funkcja wzajemnie jednoznacznie przekształcająca jeden zbiór na drugi, to te dwa zbiory są równoliczne (por. wykład X),
2. liczba podzbiorów k-elementowych zbioru n elementowego wyraża się dwumianowym symbolem Newtona i wynosi (por. wykład XI).

Przykład 12.1.1

Ile jest różnych liczb naturalnych < 2ⁿ, które w swoim zapisie w systemie binarnym mają dokładnie k jedynek?

Rozwiązanie.

Każda liczba naturalna mniejsza niż 2ⁿ w zapisie binarnym ma postać ciągu o długości co najwyżej n. Natomiast każdy ciąg n-elementowy a₀, a_1,..., a_n-1 o wyrazach a_i ∈ {0,1} można traktować jako funkcję charakterystyczną pewnego zbioru A, A ⊆ {0,1,2...,n-1}, a mianowicie:

i ∈ A wttw a_i = 1.

Zbiór A przechowuje informację na jakich pozycjach występują jedynki w ciągu a₀, a₁,..., a_n-1. Na przykład, dla n= 7 mamy 75 =(1001101)₂, a więc odpowiadający liczbie 75 zbiór, to {6,3,2,0}. Odwzorowanie, które liczbie naturalnej, przyporządkowuje zbiór numerów pozycji, na których znajdują się jedynki w binarnej reprezentacji tej liczby, jest odwzorowaniem wzajemnie jednoznacznym. Jeśli w reprezentacji binarnej pewnej liczby występuje k jedynek, to przyporządkowany tej liczbie zbiór A ma dokładnie k elementów. Zatem, liczba ciągów zerojedynkowych o długości n, w których występuje dokładnie k jedynek, jest równa liczbie wszystkich k-elementowych podzbiorów zbioru {0,1,2..., n-1}. Na mocy twierdzenia 11.5.1, takich zbiorów jest .

Przykład 12.1.2
Niech G będzie niezorientowanym grafem pełnym (tzn. takim, że każdy wierzchołek jest połączony krawędzią z każdym innym), bez pętli (tzn. nie ma krawędzi postaci (x,x)) o n wierzchołkach. Ile jest krawędzi w tym grafie?

Rozwiązanie.

Każda krawędź grafu jest wyznaczona jednoznacznie przez dwa różne wierzchołki: początek i koniec krawędzi, czyli zbiór dwuelementowy. Ponieważ, z założenia, graf jest niezorientowany, zatem (x,y) i (y,x) oznaczają tę samą krawędź. Wszystkich krawędzi jest zatem tyle ile jest dwu-elementowych podzbiorów zbioru n-elementowego. Czyli .

Oczywiście, Czytelnik zauważył, że wynik otrzymany w przykładzie 12.1.2, można było uzyskać inaczej. Wiemy przecież, że |X × Y| = |X| * |Y|. Ponieważ rozważany graf ma n wierzchołków, to uporządkowanych par wierzchołków jest n². Ponieważ interesujemy się tylko krawędziami, w których początek i koniec są różnymi wierzchołkami, to takich par mamy tylko n² - n. Na koniec, rozważany graf jest niezorientowany, a więc liczbę uzyskanych par trzeba jeszcze podzielić przez 2. Ostatecznie mamy (n²-n)/2, czyli dokładnie różnych krawędzi.

Zmodyfikujmy pytanie zawarte w przykładzie 12.1.2, i spytajmy jeszcze o liczbę dróg w grafie pełnym. Oczywiście w takim grafie występują cykle, zatem drogi możemy wydłużać w nieskończoność. Niech nasze pytanie dotyczy tylko dróg prostych (tzn. przechodzących przez różne wierzchołki) i do tego dróg, które przechodzą przez wszystkie wierzchołki grafu.

Uwaga. Drogę, przechodzącą przez wszystkie wierzchołki grafu niezorientowanego i to przez każdy dokładnie raz, nazywamy drogą Hamiltona (por. punkt 3.4).

Nasze pytanie brzmi teraz: ile różnych dróg Hamiltona można zbudować w niezorientowanym grafie pełnym o n wierzchołkach? Na początek zauważmy, że chodzi o drogi, które mają dokładnie długość n. Ponadto, dwie drogi różnią się tylko kolejnością odwiedzania wierzchołków. Zatem, istnieje wzajemnie jednoznaczna odpowiedniość między zbiorem dróg, a zbiorem permutacji liczb {1,2...n}. Wynika stąd, że w grafie pełnym jest dokładnie n! dróg Hamiltona.

Pytanie 12.1.1: Czy można podać przykład grafu niezorientowanego, w którym nie ma żadnej drogi Hamiltona?

Przykład 12.1.3

Ful w pokerze, to układ 5 kart, w których występują tylko karty o dwóch różnych wysokościach x i y, i to dokładnie 3 karty o wysokości x i 2 karty o wysokości y. Oznaczmy typ fula przez (x,y). (a) Ile jest różnych układów typu (7,D)? Pytamy więc, ile jest różnych układów 5 kart, w których trzy to siódemki, a dwie to damy.

Rozwiązanie.

Trzy siódemki zostały wybrane z zestawu 4 siódemek, które mamy w talii kart. Dwie damy zostały wybrane z zestawu 4 istniejących w talii dam. Mamy zatem możliwych wyborów siódemek i możliwych wyborów dam. Razem *, czyli 24 możliwości.

(b) Ile jest różnych typów fuli?

Rozwiązanie.

Aby ustalić jakiś konkretny typ fula (x,y), wybieramy jedną z 13 typów kart jako x, a potem dobieramy y, ale już z pozostałych 12 typów kart, zgodnie z definicją fula. Razem takich par jest więc 13*12.

Pytanie 12.1.2: Ile jest różnych zbiorów zlożonych z pięciu kart, które są fulami?

Przykład 12.1.4

W lodziarni są trzy rodzaje lodów: jogurtowe, bakaliowe i waniliowe, sprzedawane w waflach po 5 kulek. Na ile sposobów można skomponować lodowy deser, jeśli abstrahujemy od kolejności wkładania kulek do wafla?

Rozwiązanie.

Każdy deser lodowy składa się z pewnej liczby kulek jogurtowych, pewnej liczby kulek bakaliowych i z pewnej liczby kulek waniliowych. Oznaczmy je odpowiednio przez j, b i w. Z warunków zadania mamy: j ≤ 5, b ≤ 5, w ≤ 5 oraz j+b+w = 5. Każdy taki zestaw możemy bardzo prosto zakodować w 7 kratkach, z których dwie muszą być skreślone. Skreślone pozycje oddzielają od siebie grupy pustych kratek odpowiadających kulkom lodów o tym samym smaku, por. Rys. 12.1.1. Aby policzyć liczbę różnych zestawów lodów, wystarczy stwierdzić, na ile różnych sposobów możemy skreślić dwie kratki z 7 możliwych. Oczywiście, jest ich tyle, ile różnych podzbiorów dwuelementowych w zbiorze o 7 elementach. Czyli , tzn. 21.

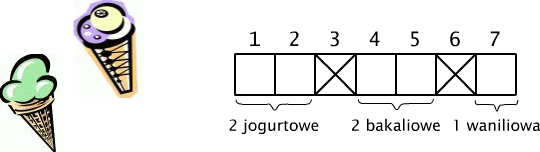
Rys. 12.1.1 Rożek z lodami i jego zakodowany opis.

Na zakończenie tego paragrafu wyjaśnimy jeszcze skąd wzięła się nazwa symbolu dwumianowego. Otóż w XVII-tym wieku Newton znalazł ogólną postać rozwinięcia n-tej potęgi dwumianu (x+y).

Wzór zawarty w twierdzeniu 12.1.1 nazywamy wzorem dwumianowym Newtona, a współczynniki występujące po prawej stronie równości w tym wzorze, to właśnie współczynniki dwumianowe Newtona.

Dla dowodu twierdzenia 12.1.1 zauważmy, że wszystkie składniki sumy, która powstaje po wykonaniu n mnożeń

są postaci (xⁱ ⋅ y^j) oraz i+j = n, tzn. z i czynników tego iloczynu wybraliśmy x, a z pozostałych wybraliśmy y. Składników postaci xⁱ y ^n-i jest dla ustalonego i dokładnie tyle, ile jest różnych sposobów wybrania i elementów ze zbioru n elementowego, czyli (n nad i). Ponieważ i może się zmieniać od 0 do n, zatem otrzymujemy dokładnie prawą stronę wzoru Newtona.

Dowód twierdzenia 12.1.1 można też przeprowadzić przez indukcję ze względu na n, pozostawiamy to jednak Czytelnikowi jako ćwiczenie.