| « poprzedni punkt | następny punkt » |
Ten punkt wykładu poświęcimy zliczaniu liczby różnych relacji binarnych określonych w skończonym zbiorze.
Niech X będzie zbiorem n elementowym. Zapytajmy najpierw, ile różnych relacji binarnych można w tym zbiorze określić. Każda relacja binarna w X jest podzbiorem produktu kartezjańskiego X × X. Wynika stąd, że relacji binarnych w X jest dokładnie tyle ile jest różnych podzbiorów produktu X × X. Ponieważ produkt X × X ma dokładnie n2 elementów, to na podstawie twierdzenia o mocy zbioru potęgowego (por. wykład 9) jest dokładnie 2n*n relacji binarnych w X.
Lemat 12.2.1
W zbiorze n elementowym można określić 2n*n relacji binarnych.
Każdą relację binarną, określoną w zbiorze skończonym, można przedstawić w postaci kwadratowej tablicy, której wiersze i kolumny są oznaczone elementami zbioru X (por. punkt 2.2). Fakt zachodzenia relacji między elementami x i y może być zaznaczony jedynką w kratce o współrzędnych (x,y). Zadanie obliczenia liczby różnych relacji binarnych sprowadza się więc do sprawdzenia, na ile sposobów można umieścić jedynki w tablicy n × n. Ale to już wiemy.
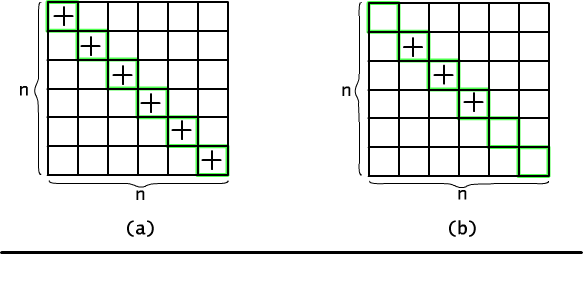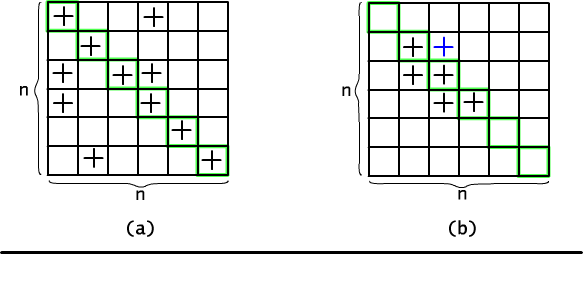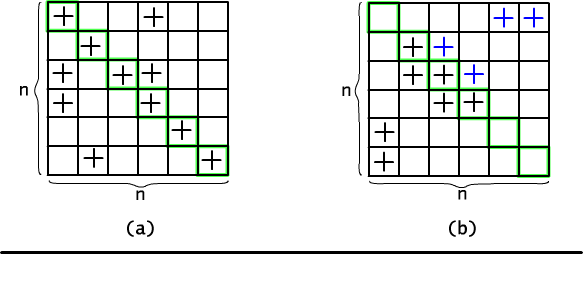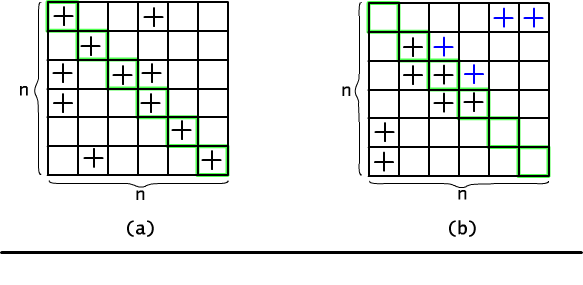
Zastanówmy się teraz, jak zmieni się rozwiązanie, jeśli chcemy policzyć tylko relacje zwrotne. Otóż, tablica incydencji, opisująca relację zwrotną, ma bardzo charakterystyczną cechę: wszystkie miejsca na głównej przekątnej są wypełnione jedynkami, por. Rys.12.2.1. Oczywiście inne miejsca w tablicy mogą być wypełnione lub nie. Czyli, aby utworzyć relację zwrotną musimy wypełnić wszystkie pozycje na przekątnej i dowolne spośród n2-n pozycji pozostałych. Odpowiedniość między relacją zwrotną i zbiorem wypełnionych kratek jest wzajemnie jednoznaczna. Zatem liczba relacji zwrotnych w zbiorze n elementowym jest równa liczbie podzbiorów zbioru (n2-n)-elementowego. Stąd dochodzimy do wniosku, że jest dokładnie 2(n-1)n relacji zwrotnych.

Rys. 12.2.1 Zliczamy relacje (a) zwrotne i (b) symetryczne.
Lemat 12.2.2
W zbiorze n-elementowym można określić 2(n-1)n relacji zwrotnych.
W podobny sposób można policzyć wszystkie relacje symetryczne. Aby zdefiniować relację symetryczną wystarczy wypełnić w dowolny sposób jedynkami pozycje na i poniżej głównej przekątnej, a potem "odbić" wybrany zbiór względem przekątnej, tzn. jeśli zaznaczona była pozycja (x,y), to dopisujemy też jedynkę na pozycji (y,x). Ponieważ początkowy wybór dotyczył tylko n(n+1)/2 par, zatem jest dokładnie 2(n+1)n/2 różnych relacji symetrycznych.
Lemat 12.2.3
W zbiorze n-elementowym można określić 2(n+1)n/2 relacji symetrycznych.
Pytanie 12.2.1: A ile relacji zwrotnych i symetrycznych można określić w zbiorze n elementowym?
Pytanie 12.2.2: Ile różnych relacji liniowego porządku można określić w zbiorze n elementowym?
| « poprzedni punkt | następny punkt » |