Ten punkt wykładu poświecimy ustaleniu liczby różnych relacji równoważności, tzn. relacji binarnych zwrotnych, symetrycznych i przechodnich. Przypomnijmy jeszcze, że każda relacja równoważności wyznacza podział zbioru, w którym została określona, na rozłączne i niepuste podzbiory, i odwrotnie, każdy podział zbioru jednoznacznie wyznacza relację równoważności, której klasami abstrakcji są właśnie zbiory danego podziału, por. wykład 5. Wynika stąd, że aby policzyć ile różnych relacji równoważności można określić w pewnym zbiorze X, wystarczy zbadać ile jest różnych podziałów tego zbioru.

Ograniczymy się w naszych rozważaniach tylko do zbiorów skończonych. Niech będzie n-elementowy zbiór X i podział tego zbioru na k zbiorów X₁, X₂,...X_k. Jak wykazaliśmy w punkcie 5.4, istnieje wzajemnie jednoznaczna odpowiedniość między podziałami zbioru na k części i relacjami równoważności w X, które posiadają k różnych klas abstrakcji.

Wprost z definicji wynika, że

S(n,k) = 0, gdy k>n, S(n,n) =1, S(n,1) = 1, S(n,0) = 0 dla n>0.

Zanim zbadamy własności liczby S(n,k) w przypadku ogólnym, przyjrzyjmy się przykładom.

Przykład 12.3.1

1. Zbiór {1,2,3} ma trzy możliwe podziały na 2 bloki:

   {{1}, {2,3}}, {{2}, {1,3}},{{3}, {1,2}}.

   Ten sam zbiór ma tylko jeden możliwy podział na 3 części, a mianowicie {{1}, {2}, {3}}. Odpowiadające tym podziałom liczby Stirlinga wynoszą S(3,2) = 3, S(3,3) = 1.

2. Zbiór {a, b, c, d} ma aż 7 różnych podziałów na 2 części:

   {{a,b},{c,d}}, {{a,c},{b,d}},{{a,d}, {b,c}},

   {{a,b,c}, {d}},{{a,b,d}, {c}},{{a,c,d}, {b}},{{c,b,d}, {a}}.

   Zatem S(4,2) = 7.

Załóżmy, że rozważany przez nas zbiór n-elementowy X składa się z liczb naturalnych 1, 2,..., n. Wszystkie podziały tego zbioru na k bloków (części) można podzielić na dwa typy:

• podziały, które zawierają blok jednoelementowy {n},

• podziały, w których liczba n występuje w większych blokach.

Jeśli mamy podzielić zbiór n-elementowy na k części, ale ustalimy równocześnie, że jedną z tych części jest zbiór jednoelementowy {n}, to pozostałe elementy trzeba rozdzielić na k-1 bloków. Zatem, liczba podziałów, w których jedna z części to zbiór jednoelementowy {n}, wynosi S(n-1, k-1).

Jeśli natomiast rozważamy podziały, w których liczba n nie może sama tworzyć bloku, to wystarczy wziąć dowolny podział zbioru (n-1)-elementowego na k bloków i do jednego z nich dopisać liczbę n. Liczbę n możemy dopisać na k sposobów, a podziałów zbioru (n-1)-elememtowego na k części jest S(n-1, k). Razem k* S(n-1, k) podziałów. Wynika stąd następująca zależność rekurencyjna:

S(n,k) = S(n-1, k-1) + k* S(n-1,k). (*)

Korzystając kilkakrotnie z tego wzoru, z łatwością wyliczymy na przykład, że S(7,3) = 301.

Rzeczywiście,

S(7,3) = S(6,2) + 3*S(6,3) = [S(5,1) + 2*S(5,2)] + 3*[S(5,2) + 3*S(5,3)] = S(5,1) + 5*S(5,2) + 3² * [S(4,2) + 3 * S(4,3)] = ... = S(5,1) + 5*S(4,1) + 19*S(3,1) + 65*S(2,1) + 130*S(2,2) + 81*S(3,3) = 301.

Wróćmy teraz do problemu relacji równoważności. Relacja równoważności określona w zbiorze skończonym n-elemenowym może mieć i klas abstrakcji, gdzie i = 1, 2, ..., n. Ponieważ różnych relacji równoważności posiadających i klas abstrakcji jest tyle ile podziałów zbioru n-elementowego na i bloków, zatem zachodzi następujące twierdzenie:

Wydaje się, że wyliczenie wartości S(n,k) dla danych liczb n i k nie przedstawia dużego problemu, szczególnie, jeśli możemy użyć do tego celu komputera. Wzór (*) sugeruje bardzo prosty rekurencyjny algorytm. Niestety, podobnie jak w przypadku trójkąta Pascala, nie można tu użyć rekursji (dlaczego?). Można natomiast użyć pomocniczej tablicy aby zapamiętać wcześniej wyliczone wartości. Ustawmy wartości S(n,k) w postaci trójkątnej tablicy, zwanej trójkątem Stirlinga, tak jak na rysunku Rys. 12.3.1

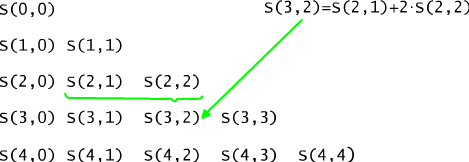
Rys. 12.3.1 Trójkąt Stirlinga

Wypełnienie pozycji S(n,k) w n-tym wierszu i k-tej kolumnie trójkąta Stirlinga polega na dodaniu do siebie liczby S(n-1,k-1) (z poprzedniego wiersza i poprzedniej kolumny) i, pomnożonej przez k, liczby S(n-1,k) (z poprzedniego wiersza i tej samej kolumny). Wyliczenie wartości w jakimś wierszu wymaga więc wyliczenia i zapamiętania wartości z wiersza poprzedniego. Algorytm wypełniający fragment tego trójkąta (do k-tej kolumny) może wyglądać następująco

Algorytm ten jest bardzo prosty, jednak nie na wiele się przyda, ponieważ liczby Stirlinga rosną niezwykle szybko.

Pytanie 12.3.1: Na ile sposobów można przedstawić liczbę 7 w postaci sumy a+b+c, gdzie każda z cyfr a, b, c jest różna od zera (układy różniące się kolejnością uznajemy za różne)? Dlaczego odpowiedzią nie jest S(7,3)?