| « poprzedni punkt | następny punkt » |
Niech X będzie dyskretną zmienną losową określoną w przestrzeni Ω.
Definicja 14.2.1
Funkcję fX określoną na zbiorze liczb rzeczywistych R i o wartościach w zbiorze [0,1] taką, że fX(x) = P(X=x) dla x ∈ R nazywamy rozkładem prawdopodobieństwa zmiennej losowej X.
Przykład 14.2.1
Rozważmy zmienne X, Y, Z rozpatrywane w przykładzie 14.1.2 z rzutem dwiema kostkami do gry. Zbiór wartości zmiennych X i Y, to liczby 1, 2, ..., 6. Natomiast zbiór wartości zmiennej Z to {2, 3, 4, ..., 11, 12}. Prawdopodobieństwo z jakim zmienne przyjmują swoje wartości opisują funkcje fX , fY i fZ, por. Rys.14.2.1
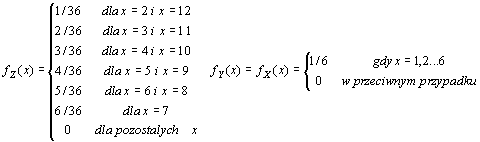

Rys. 14.2.1 Rozkład prawdopodobieństwa zmiennej losowej Z, której wartością jest suma wyrzuconych oczek, w doświadczeniu polegającym na rzucie dwiema kostkami sześciennymi do gry.
Przykład 14.2.2
Rzucamy n-krotnie symetryczną monetą. Niech Xi będzie zmienną losową przyjmującą wartości 0 i 1 w zależności od tego co wypadło w i-tym rzucie:
Xi = 1 wttw w i-tym rzucie wypadł orzeł,
Xi = 0 wttw w i-tym rzucie wypadła reszka.
Mamy P( Xi = 1) = P( Xi = 0) = 1/2, zatem rozkład prawdopodobieństwa zmiennej Xi ma postać fXi(x) = 1/2 dla x=1 i x=0 (Oczywiście w pozostałych przypadkach fXi(x)=0) dla i=1,2,..., n.
Rozważmy zmienną losową Sn = X1 + X2 +...+ Xn. Zmienna ta podaje liczbę orłów w n rzutach monetą. Wartościami tej zmiennej losowej są liczby 0,1,2,...,n. Prawdopodobieństwo wyrzucenia k orłów w n rzutach monetą wynosi
P(Sn = k) = (n nad k)/ 2 n
Zatem, rozkład prawdopodobieństwa zmiennej losowej Sn ma postać
Przedstawiony rozkład prawdopodobieństwa jest szczególnym przypadkiem rozkładu zwanego rozkładem dwumianowym fSn(k) = P(n, k, 1/2). Spotkaliśmy się z nim przy omawianiu schematu Bernoulliego.
Przykład 14.2.3
Rozważmy doświadczenie polegające na serii niezależnych rzutów symetryczną monetą powtarzanych dopóty, dopóki nie wypadnie orzeł. Niech W będzie zmienną losową, której wartością jest "czas oczekiwania" na orła, a dokładniej, liczba wykonanych prób do chwili uzyskania orła. Wartością zmiennej W jest liczba k, jeśli w k-1 pierwszych rzutach wypadła reszka, a w k-tym rzucie wypadł orzeł. Zmienna W przyjmuje jako wartości wszystkie liczby naturalne. Rozkład prawdopodobieństwa tej zmiennej ma postać
f(k) = P(W=k) = (1/2)(1/2)k-1= 1/2k.
Rozkład prawdopodobieństwa zmiennej W jest szczególnym przypadkiem rozkładu geometrycznego.
Definicja 14.2.3
Rozkład prawdopodobieństwa określony wzorem f(k) = p(1-p)k-1 nazywamy rozkładem geometrycznym.
Na zakończenie tej części wykładu rozważmy jeszcze jeden prosty przykład zmiennej losowej. Niech zmienna losowa X określa liczbę wyrzuconych oczek w rzucie kostką sześcienną do gry. Wartościami tej zmiennej są po prostu liczby 1, 2, 3, 4, 5, 6. Przy założeniu symetrii kostki, prawdopodobieństwo wyrzucenia dowolnej z wymienionych wartości wynosi 1/6 i jest równe 0 dla wszystkich pozostałych liczb rzeczywistych. Rozkład prawdopodobieństwa zmiennej X jest przykładem rozkładu jednostajnego.
Definicja 14.2.4
Rozkład prawdopodobieństwa dyskretnej zmiennej losowej nazywamy jednostajnym, jeśli przybiera ona wszystkie swoje wartości z takim samym prawdopodobieństwem.
Przykład 14.2.4
Dwaj gracze grają w orła i reszkę. Jeśli wypadnie orzeł gracz G1 płaci graczowi G2 złotówkę. Jeśli wypadnie reszka, to gracz G2 płaci graczowi G1 złotówkę. Zmienna losowa X opisująca wygraną gracza G1 przyjmuje następujące wartości X(O) = -1, X(R) = +1. Przy założeniu symetrii monety, mamy P(X=-1) = 1/2 i P(X=1) = 1/2. Zmienna X ma rozkład jednostajny.
Pytanie 14.2.1 Jaki jest rozkład prawdopodobieństwa zmiennej losowej X, która podaje liczbę wykonanych rzutów symetryczną kostką sześcienną do chwili uzyskania po raz pierwszy szóstki?
Zobacz odpowiedź
| « poprzedni punkt | następny punkt » |