Definicja 14.3.1

Niech X będzie zmienną losową określoną na dowolnej przestrzeni zdarzeń losowych Ω. Dystrybuantą zmiennej X nazywamy funkcję F : R → [0,1] taką, że

F_X(x) = P(X ≤ x) dla x ∈ R.

Pytanie 14.3.1 Jeśli a jest największą wartością jaką przyjmuje zmienna losowa X, to jaka jest wartość jej dystrybuanty w punkcie a?

Zgodnie z powyższą definicją, dystrybuanta zmiennej losowej akumuluje wartości rozkładu prawdopodobieństwa. Sprawdzimy to na przykładach.

(a) Rozważmy doświadczenie z rzutem jedną kostką sześcienną do gry i zmienną losową opisującą liczbę wyrzuconych oczek. Ponieważ wartości jakie przyjmuje ta zmienna dyskretna to liczby naturalne 1, 2, 3, 4, 5, 6, a rozkład prawdopodobieństwa jest jednostajny (przy założeniu symetrii kostki), to dystrybuanta wyraża się wzorem F_X(x) = 0 dla x<1 F_X(x) = i ⋅ (1/6) dla i ≤ x <(i+1) oraz i=1,2,3,4,5 , F_X(x) = 1 dla x ≥ 6 (por. Rys.14.3.1).

(b) Pewien test składa się z 5 pytań. Do każdego pytania zaproponowano 4 różne odpowiedzi do wyboru, ale tylko jedna z nich jest poprawna. Niech Y będzie zmienną losową podającą liczbę dobrych odpowiedzi w doświadczeniu polegającym na przypadkowym zakreśleniu jednej odpowiedzi w każdym pytaniu. Zmienna Y przyjmuje tylko wartości 0, 1, 2, 3, 4, 5. Przyjmijmy, że prawdopodobieństwo zakreślenia dobrej odpowiedzi w jednym pytaniu wynosi 1/4. Oczywiście mamy tu do czynienia ze schematem Bernoulliego dla n = 5 i p = 1/4.
Ponieważ f_Y(k) = P(n,k,p) = (ⁿ_k) ⋅ p^k ⋅ (1-p)^n-k dla k=0,1,2...5, zatem

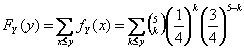
W tabeli Rys. 14.3.2 podano wartości funkcji rozkładu prawdopodobieństwa tej zmiennej i jej dystrybuantę.

Rys. 14.3.1 Dystrybuanta zmiennej losowej określającej liczbę wyrzuconych oczek w rzucie jedna kostką sześcienną do gry.

Rys. 14.3.2 Rozkład prawdopodobieństwa oraz dystrybuanta zmiennej Y, por. przykład 14.3.1(b).

Lemat 14.3.1

Dystrybuanta zmiennej losowej dyskretnej jest funkcją niemalejącą. Co więcej, dystrybuanta zmiennej losowej rośnie skokowo w punktach należących do zbioru wartości tej zmiennej.

Niech F(x) będzie dystrybuantą dyskretnej zmiennej losowej X. Jeśli x'<x" dla pewnych wartości x' i x" zmiennej losowej X, to

Każdy z n myśliwych strzela do jednego z n zajęcy (wybranego losowo). Oznaczmy przez X zmienną losową określającą liczbę zajęcy, do których nikt nie strzelał. Zakładamy, że każdy myśliwy z takim samym prawdopodobieństwem wybiera zająca, do którego oddaje strzał, i, że jego wybór jest niezależny od tego co zrobią inni myśliwi. Przestrzeń zdarzeń elementarnych Ω składa się z wszystkich ciągów n elementowych o wartościach w zbiorze n-elementowym: pozycja ciągu oznacza strzelca, a wartość - numer zająca, do którego oddano strzał. Ω składa się więc z wszystkich funkcji ze zbioru n-elementowego w zbiór n-elementowy, zatem | Ω | = nⁿ.

Niech zadanie polega na znalezieniu rozkładu prawdopodobieństwa i dystrybuanty zmiennej losowej X, w przypadku gdy n = 5.

Zmienna X przyjmuje jako wartości liczby 0 (strzelano do wszystkich zajęcy), 1, 2, ..., (n-1) ( przypadek, gdy wszyscy strzelają do tego samego zająca). Policzmy P(X=i), czyli prawdopodobieństwo tego, że nie strzelano do i spośród n zajęcy. Inaczej mówiąc, szukamy prawdopodobieństwa tego, że wybrana losowo funkcja f ∈ Ω spełnia |Im(f)|=n-i. Mamy (n nad i) możliwych wyborów i elementów z n-elementowego zbioru. Skoro nie strzelano do i zajęcy, to strzelano do dokładnie n-i zajęcy. n myśliwych może oddać strzał do n-i zajęcy na tyle sposobów, ile jest funkcji ze zbioru n-elementowego na zbiór (n-i)-elementowy. Na mocy rozważań w wykładzie 12tym, takich funkcji jest dokładnie (n-i)! S(n,n-i), gdzie S(n,n-i) oznacza liczbę Stirlinga drugiego rodzaju. Mamy więc ostatecznie

Z powyższych obliczeń wynika, że rozkład prawdopodobieństwa i dystrybuanta rozważanej zmiennej losowej mają odpowiednio postać:

Pytanie 14.3.1 Niech X będzie zmienną losową, której wartością jest suma oczek wyrzuconych w rzucie dwoma symetrycznymi kostkami sześciennymi. Jaka jest wartość dystrybuanty tej zmiennej w punkcie x = 4.5?

^k	⁰	¹	²	³	⁴	⁵
^P(X=k)*¹⁰²⁴	²⁴³	⁴⁰⁵	²⁷⁰	⁹⁰	¹⁵	¹
^{P(X ≤ k)*1024}	²⁴³	⁶⁴⁸	⁹¹⁸	¹⁰⁰⁸	¹⁰²³	¹⁰²⁴