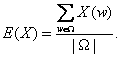
| « poprzedni punkt | następny punkt » |
Jednym z podstawowych parametrów rozkładu prawdopodobieństwa jest wartość oczekiwana zmiennej losowej.
Definicja 14.4.1
Niech Ω będzie przestrzenią zdarzeń elementarnych, a X zmienną losową określoną w Ω. Wartością oczekiwaną zmiennej X nazywamy liczbę
E(X) = Σ w ∈ Ω X(w) ⋅ P({w}).
Uwaga Jeśli wszystkie zdarzenia elementarne są jednakowo prawdopodobne, a przestrzeń Ω jest skończona, to P({w}) = 1/| Ω|, a wtedy
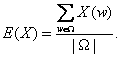
Zatem w tym przypadku, wartość oczekiwana jest równa średniej arytmetycznej wartości przyjmowanych przez zmienną X.
Zauważmy, że wartość oczekiwana nie musi być równa żadnej z wartości przyjmowanych przez zmienną losową.
Lemat 14.4.1
Niech X będzie zmienną losową dyskretną określoną w pewnej przestrzeni zdarzeń elementarnych Ω oraz niech (xi)i ∈ I będzie ciągiem wszystkich różnych wartości jakie przyjmuje ta zmienna. Jeżeli suma Σ i ∈ Ι (xi ⋅ P(X=xi)) jest określona, to
![]()
Dowód.
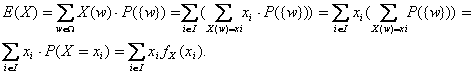 ♦
♦
Przykład 14.4.1
(a) Rzucamy jedną kostką do gry. Liczba wyrzuconych oczek X jest zmienną losową o wartościach 1,2,3,4,5,6 i ma rozkład jednostajny P(X = i) = 1/6. Zatem
E(X) = 1(1/6) + 2(1/6) + 3(1/6)...+ 6(1/6) = (1+2+3+4+5+6)/6 = 3.5
(b) Niech Y będzie zmienną opisującą liczbę trafnych odpowiedzi w teście złożonym z 5 pytań, por. przykład 14.3.1. Tabelka 14.3.2 przedstawia rozkład tej zmiennej. Na podstawie tej tabelki wyliczmy wartość oczekiwaną zmiennej Y:
E(Y) = (0 ⋅ 243 +1 ⋅ 405 +2 ⋅ 270 + 3 ⋅ 90 + 4 ⋅ 15 +5 ⋅ 1)/1024 = 1280/1024 = 1.27.
(c) W tramwaju zgasło światło. Pewien pasażer, który miał w kieszeni
15 biletów skasował losowo wyciągnięty bilet. Jaka jest wartość
oczekiwana jego opłaty za przejazd, jeśli wiadomo, że pasażer miał 5
biletów po 1.20 zł., cztery bilety po 2.40 zł. i sześć biletów po 4.80
zł.?
Rozkład prawdopodobieństwa zmiennej Z, opisującej uiszczoną opłatę za
przejazd określają równości:
fZ(1.20) = 5/15, fZ(2.40) = 4/15, fZ(4.80)
= 6/15.
Stąd wartość oczekiwana opłaty wynosi
E(Z) = 1,20 ⋅ 5/15 + 2,40 ⋅ 4/15+ 4,80 ⋅ 6/15 = 2,96.
Przykład 14.4.2
W pewnej loterii sprzedaje się n losów, z których n1 wygrywa sumę x1 zł., n2 - wygrywa x2 zł., ..., nk losów wygrywa xk zł. Loterię nazywamy sprawiedliwą, jeśli suma wygranych jest równa ilości pieniędzy uzyskanych ze sprzedaży biletów. Zbadajmy, jaka powinna być cena jednego losu, żeby loteria była sprawiedliwa.
Zmienna losowa X przypisująca losowi wygraną przyjmuje k wartości x1,
x2, ..., xk, i przy założeniu, że każdy los może
zostać kupiony z takim samym prawdopodobieństwem, ma rozkład
prawdopodobieństwa postaci:
Jeśli c oznacza szukaną cenę biletu, to mamy
n ⋅ c = Zysk = Suma wygranych = x1 ⋅ n1 + x2 ⋅ n2 +...+ xk ⋅ nk.
Stąd c = x1 ⋅ (n1 /n ) + x2 ⋅ (n2 /n)+...+ xk ⋅ (nk/n) = x1 ⋅ f(x1) + x2 ⋅ f(x2)+...+ xk ⋅ f(xk) = E(X).
Wynika stąd, że loteria będzie sprawiedliwa, jeśli cena biletu będzie równa wartości oczekiwanej zmiennej losowej opisującej wygraną dla jednego losu.
Pytanie 14.4.1 Jaka jest wartość oczekiwana zmiennej losowej opisującej sumę wyrzuconych oczek w rzucie dwoma symetrycznymi kostkami sześciennymi?
Wartość oczekiwana zmiennej dyskretnej określonej w skończonej przestrzeni zdarzeń elementarnych jest skończoną sumą liczb rzeczywistych i zawsze istnieje. Jeśli zmienna losowa przyjmuje tylko skończoną liczbę wartości, to jej wartość oczekiwana jest dobrze określoną liczbą rzeczywistą. Jeśli natomiast zmienna losowa przyjmuje nieskończenie wiele wartości, to może się zdarzyć, że wartość oczekiwana tej zmiennej nie istnieje.
Przykład 14.4.3
Rozważmy zmienną losową X, która przyjmuje wartości xi = 2i-1 dla i =1, 2, 3 ... z prawdopodobieństwem P(X= xi) = 1/2i. Wtedy
![]()
Ponieważ ta ostatnia suma jest nieskończona, zatem nie istnieje wartość oczekiwana dla rozważanej zmiennej.
Niech Ωbędzie ustaloną przestrzenią zdarzeń, w której mamy określone dwie zmienne losowe dyskretne X i Y. Suma zmiennych losowych X i Y jest zmienną losową Z, określoną dla dowolnego zdarzenia elementarnego w tej przestrzeni jako Z(w) = X(w)+Y(w). Jeśli zmienna X przyjmuje wartości xi dla i ∈ I, a zmienna Y przyjmuje wartości yj dla j ∈ J, to zmienna Z przyjmuje jako swoje wartości liczby (xi + yj) dla dowolnych i ∈I i j ∈J.
Po tych wyjaśnieniach możemy przejść do sformułowania twierdzenia charakteryzującego wartość oczekiwaną zmiennej losowej.
Twierdzenie 14.4.1
Niech Ω będzie przestrzenią zdarzeń, w której określone są zmienne losowe X i Y. Jeśli wartości oczekiwane zmiennych X i Y istnieją, to dla dowolnego c zachodzą równości
Dowód.
Dla dowodu równości (b) przyjmijmy, że zmienna losowa X przyjmuje wartości xi dla i ∈ I, a zmienna Y przyjmuje wartości yj dla j ∈ J.
![]()
![]()
![]()
Ponieważ wewnętrzne sumy redukują się do P(X = xi) i P(Y = yj) odpowiednio, to
![]()
Dowody pozostałych własności pozostawiamy Czytelnikowi. ♦
Analogicznie jak sumę zmiennych, można zdefiniować iloczyn zmiennych losowych X i Y określonych w tej samej przestrzeni Ω. Przyjmujemy Z(w) = X(w) ⋅ Y(w) dla w ∈ Ω. Zmienna Z przyjmuje jako swoje wartości iloczyny xi ⋅ yj dla i ∈ I i j ∈ J, jeśli xi i yj są wartościami zmiennych X i Y, odpowiednio.
Twierdzenie 14.4.2
Jeśli X i Y są niezależnymi zmiennymi losowymi, to E(X ⋅ Y) = E(X) ⋅ E(Y).
Dowód.
Na mocy definicji:
![]()
Ponieważ z założenia zmienne X i Y są niezależne, zatem P(X=xi, Y=yj) = P(X=xi) ⋅ P(Y=yj) .
Stąd mamy
![]()
Pytanie 14.4.2: Jeśli zmienna losowa przyjmuje dla wszystkich zdarzeń elementarnych w rozważanej przestrzeni tę samą wartość c, to jaka jest wartość oczekiwana tej zmiennej?
| « poprzedni punkt | następny punkt » |