| « previous section | next section » |
This section will be devoted to the binary relations such that their domains and co-domains are included in the same set.
Definition 2.3.1
A binary relation r ⊆ X × X is called reflexive iff for every x ∈ X, (x, x) belongs to r.
A binary relation r ⊆ X × X is irreflexive iff for every x ∈ X, (x, x) does not belong to r .
It follows from the above definion that, if a binary relation is
defined on a set X, then
r is reflexive iff {(x, x) : x ∈ X } ⊆ r,
r is irreflexive iff {(x, x) : x ∈ X } ∩ r = ∅.
The most characteristic example of an reflexive relation is equality = in arbitrary set X. This relation consists solely of the ordered pairs (x,x) for all x in X. Another well known reflexive relation is "greater than or equal to". Contrary to this, "greater than" relation is not reflexive, and is irreflexive, since no pair of the form (x,x) belongs to it.
Let us see, what the matrix of the reflexive relation looks like. Since every x is in the relation with itself then all positions on the main diagonal must be marked. The other positions may or may not be marked. We can easily recognize a reflexive relation defined on a finite set by looking on its grahical illustration: a relation is reflexive if for every vertex there is an edge going back to this same vertex (it is known as a loop).
In the case of the irreflexive relation, none of the positions in the main diagonal in the matrix can be marked and none of the vertices has a loop.
Example 2.3.1
Let us consider the relation "to be divisible" | in the set {1,2,3,4,5,6,7,8,9}. Recall that | is defined as: x|y iff y is divisible by x. This relation is reflexive, since each number is divisible by itself. The matrix of this relation as well as its graph are presented on the Fig. 2.3.1.
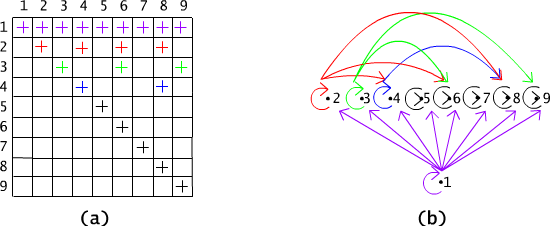
Fig. 2.3.1 Graph of the relation "to be divisible" in the set {1,2,3,4,5,6,7,8,9}.
Observe that a binary relation can be neither reflexive and nor irreflexive at the same time. These two notions are not opposite. Figure 2.3.2 presents an example of such a relation:
it is not reflexive since an ordered pair (6,6) does not belong to it, and
it is not irreflexive, since, for example the ordered pair (1,1) belongs to it.
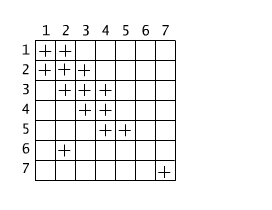
Fig. 2.3.2 An example of the relation which is neither reflexive and nor irreflexive.
Question 2.3.1 Given a square table (matrix) the row and columns of which are numbered with natural numbers from 0 to 9 and which elements are zeroes and ones, which property is verified by the following algorithm?
{i:=0; result := true;
while (i<10 and result) do
if T[i,i] = 0 then result := false; fi;
i := i+1;
od }
Definition 2.3.2
A binary relation r ⊆ X × X is called symmetric iff for all x, y ∈X, if the pair (x,y) is in r, then the pair (y,x) is also in r. A binary relation in X is called asymmetric iff for every x and y from the set X, if (x, y) ∈ r then (y, x) ∉ r.
As an example of the symmetric relation we can take the relation "to be parallel" defined in the set of all straight lines on the plane || :
l1 || l2 iff the line l1 is parallel to the line l2.
Relation < in the set of real numbers, is not symmetric, and is asymmetric: if x < y, then it is not the case y < x.
One can easly recognize both types of relations simply from the matrix or from the graph of the relation: the matrix of any symmetric relation is symmetric with respect to the main diagonal, see Fig. 2.3.3(a), and the graph of a symmetric relation has all edges in both directions, see Fig. 2.3.3(b).
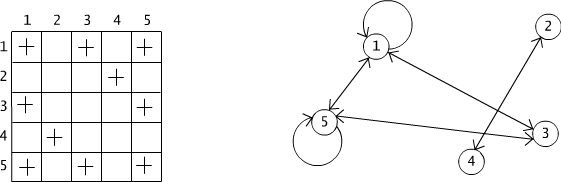
Fig. 2.3.3 (a) Matrix of the symmetric relation and (b) its graph.
Let us see that a relation can be neither symmetric nor asymmetric at the same time, as it is in the case of the relation presented on the Fig. 2.3.2. It is not symmetric since (5,4) belongs to the relation and (4,5) does not. It is not asymmetric since both pairs (4,3) and (3,4) belong to this relation.
Definition 2.3.3
A binary relation r in X, ⊆ X × X ie called antisymmetric iff for arbitrary x, y ∈ X, if both pairs (x, y) i (y, x) are in r, then x = y.
The relation ≤ in the set of real numbers and the divisibility relation in the set of natural numbers are examples of antisymmetric relations. Observe that a relation can be at the same time symmetric and antisymmetric, as it is in the case of identity relation, and any relation that is a subset of identity.
Definition 2.3.4
A binary relation r ⊆ X × X is called transitive iff for every x, y, z ∈ X, if (x,y) ∈ r and (y,z) ∈ r, then (x, z) ∈ r.
The simple examples of transitive relations are < and ≤ in the set of all real numbers. Several other examples we shall see in the next sections of the lecture.
Question 2.3.2 Is each irreflexive and transitive relation
asymmetric?
Example 2.3.2
Let X be the set of all points of the plane. Denote by p.x and p.y
the coordinates of a point p and let r be a binary relation defined as
follows:
p r q iff (p.x)2 + (p.y)2
= (q.x)2 + (q.y)2 for arbitrary points p
and q .
The relation defined in this way
is reflexive, since (p.x)2 + (p.y)2 = (p.x)2 + (p.y)2,
is symmetric, since (p.x)2 + (p.y)2 = (q.x)2 + (q.y)2 implies (q.x)2 + (q.y)2 = (p.x)2 + (p.y)2,
is transitive, since when p r q and q r w then by definition (p.x)2 + (p.y)2 = (q.x)2 + (q.y)2 and (q.x)2 + (q.y)2 = (w.x)2 + (w.y)2 . Form that by transitivity of = we have (p.x)2 + (p.y)2 = (w.x)2 + (w.y)2.
Question 2.3.3 Let r be a binary relation defined by
formula:
Is the relation r transitive?
| « previous section | next section » |