Now we are going to deal with a problem of the counting number of equivalence relations i.e. binary, reflexive, symmetric as well as transitive relations. Notice that every equivalence relation over an arbitrary set  X determines its partition into disjoint non-empty blocks that cover all of X, and vice versa, every set's partition determines the equivalence relation (see lecture 4).
Observation. To count the number of equivalence relations over some set X one may count the number of different set's partitions.

We restrict our considerations to finite sets only. Let be given an n-element set X and its partition into k blocks X₁, X₂, ..., X_k. As we know from the subsection 4.4, there exists a mutually unambiguous correspondence between k-parts partitions and equivalence relations over the set X which have k different abstraction classes.

According to this definition, we can conclude that

S(n,k) = 0, when k>n, S(n,n) =1, S(n,1) = 1, S(n,0) = 0 for n>0.

Before we do more precise research into Stirling's numbers S(n,k) we want to analyse a few examples.

Example 12.3.1

1. Set {1, 2, 3} has three different partitions into 2 blocks:

   {{1}, {2,3}}, {{2}, {1,3}},{{3}, {1,2}}.

   This set has only one division into 3 blocks, i.e. {{1}, {2}, {3}}. Stirling's numbers of the second kind adequate to these partitions are: S(3,2) = 3, S(3, 3) = 1.

2. Set {a, b, c, d} has seven different partitions into 2 blocks:

   {{a,b},{c,d}}, {{a,c},{b,d}},{{a,d}, {b,c}},

   {{a,b,c}, {d}},{{a,b,d}, {c}}, {{a,c,d}, {b}},{{c,b,d}, {a}}.

   Thus, S(4,2) = 7.

Let's assume that the considered n-element set is built with natural numbers from 1 to n. All set's partitions into k blocks may be divided on into two types:

(a) partitions which include a 1-element block {n},

(b) partitions in which  n occurs in more-than-one-element blocks.

If we want to divide an n-element set into k blocks with an assumption that one of these parts is {n}, then the remaining elements must be split into k-1 blocks. Therefore, a number of such  partitions is   S(n-1, k-1).

Now, if we consider case (b) then it is enough to take all k-element partitions  of the (n-1)-element set into k blocks  (we omit the number n) and after that add n  to one of blocks in each partition. Of course, the number n may be added in k different ways to each partition.  As the number of partitions of the (n-1)-element set into k blocks is equal to S(n-1, k),  summing up all, we obtain k* S(n-1, k) partitions of the type (b).
It implies the following recursive equation

S(n,k) = S(n-1, k-1) + k* S(n-1, k). (*)

Using it a few times we may easily derive that  S(7,3) = 301. Indeed:

S(7,3) = S(6,2) + 3*S(6,3) = [S(5,1) + 2*S(5,2)] + 3*[S(5,2) + 3*S(5,3)] = S(5,1) + 5*S(5,2) + 3² * [S(4,2) + 3 * S(4,3)] = ... = S(5,1) + 5*S(4,1) + 19*S(3,1) + 65*S(2,1) +130*S(2,2) + 81*S(3,3) = 301.

Let's go back to the equivalence relations problem. It is obvious that an equivalence relation over an n-element set has or one or two or ..., n abstraction classes. Hence, according to the observation  above, the following theorem holds:

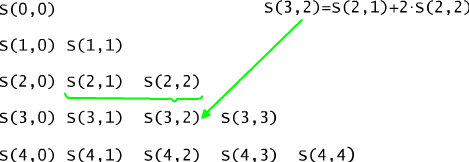
The sum in the above mentioned theorem is known as the Bell number B(n). It seems that counting S(n,k) values for arbitrary n and k is not a very complicated task, especially when we use a computer. Equation (*) implies an easy recursive algorithm. Unfortunately, as it is in the Pascal's triangle case, we cannot use the recursive method here (why?). To go around this problem, we should use an auxiliary triangular matrix to memorise values computed in advance. We order S(n,k) values in the manner called Stirling's triangle, see Figure 12.3.1.

Fig. 12.3.1 Stirling's triangle.

In order to fill  up the S(n,k) position in the n-th row and k-th column we add value S(n-1,k-1) (previous row and previous column) multiplied by k to S(n-1,k) (previous row, the same column). Therefore, to fill up a row of the matrix we  need  knowledge about  values in the previous row. An algorithm which does this task (fills a Stirling's triangle up to the k-th column) may be implemented as follows:

This algorithm is easy but also very impractical. That is because Stirling's numbers grow extremely fast.

 
Question 12.3.1 Find a formula for the number of ways to distribute r distinct persons into n different initially empty rooms, so that exactly m  rooms were non-empty, m< n.