Surjection is as you remember an "onto" mapping. Let's assume f to be a function from some finite set X to some set Y such that the cardinality of X is at least equal to the Y cardinality, i.e. |Y| ≤ |X|.

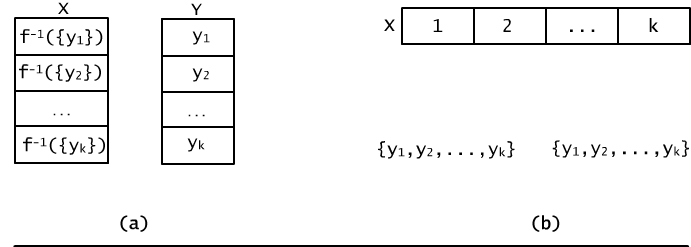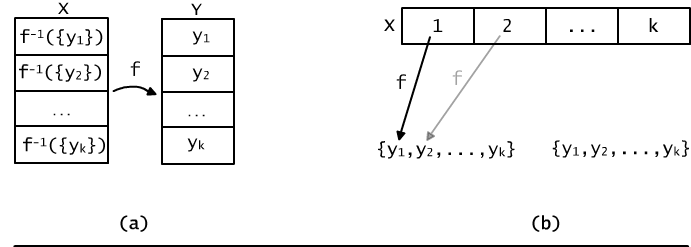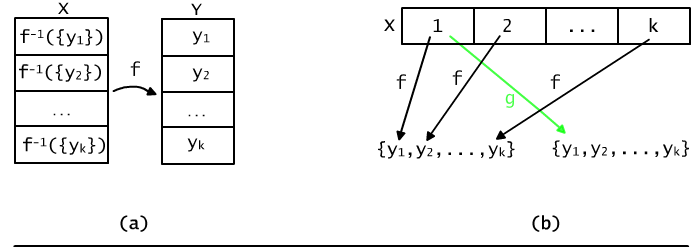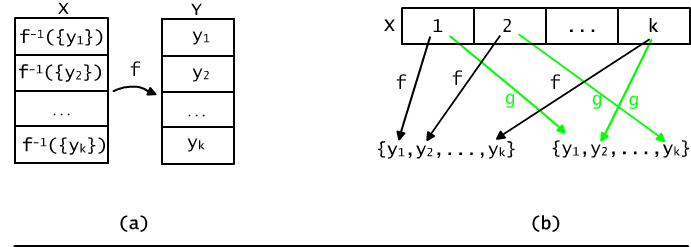
Notice, that if Y = {y₁, y₂, ..., y_k} and we are given the integer function f: X → ^onto Y, then putting  X _i = f ^-1({y_i}) for i = 1, 2, ..., k we obtain a partition of the set X into k blocks (see Figure 12.4.1(a)).

Indeed, if the sets X_i and X_j for i ≠ j have a shared element x, then, according to the definition (see lecture 3), it would be f(x) = y_i as well as f(x) = y_j which is impossible since f is a function. Hence for i ≠ j , the sets X_i and X_j  are disjoint. Because f is a surjection, then every element of the set Y is a value for some element of the set X. Thus, all sets  X_i for i = 1,2 ..., n are non-empty. Moreover, as soon as f is a total function then every element x has a value in Y.  Summing up all sets X₁,..., X_k, we obtain the set X.

Fig. 12.4.1 (a) Function f determines a partition of the set X. (b) Arbitrary partition of the set X into k blocks determines k! different functions onto the k-element set.

On the other hand, if we are given a partition of X into k blocks X₁, ..., X_k then, ascribing them elements' of Y, we define the function from X onto Y (see Fig. 12.4.1b). For example, we can define such a function in the manner presented below:

Because sets X₁, ..., X_k are pair-disjoint, we obtain a well defined function f. The way of choosing element y_i for set X_i  is accidental. Truly speaking, we may use any other element of Y. Therefore, we have k! (all permutations of Y set's elements) different functions which apply to the same partition.

Because the number of partitions of an n-element set X into k blocks is equal to the Stirling's number S(n,k) we can formulate the following conclusion:

Question 12.4.1 In how many ways can we split 5 different sweets between 3 children in such a way that each of them gets at least one sweet?

« previous section

« next section