« previous section  « next section 


12.5  Inclusion-exclusion principle

Now we are going to present a problem which seems to be very easy and yet is not. Let X1, ..., Xn  be finite sets, and X = X1 ∪ ... ∪ Xn. How the number of elements of the set X depends on the number of elements of  X1,...,Xn ?

Firstly, we consider a simple case when n = 2, i.e. X = X1 ∪ X2, see Figure 12.5.1a.

Example 12.5.1

  1. X1 = {1,2}, X2 = {3,4,5}. Then |X1 ∪ X2| = |{1,2,3,4,5}| = |X1 | + |X2| = 2 + 3 = 5.
  2. X1 = {1,2,3}, X2 = { 2,3,4,5}. Then |X1 ∪ X2| = |{1,2,3,4,5}| = 5  ≠ |X1 | + |X2| = 3 + 4 .

If the sets X1, X2 are disjoint then |X| = |X1| + |X2|, if not, then the sum |X1| + |X2| counts shared elements two times. This argument leads to the following conclusion:

Lemma 12.5.1

For any sets X1 , X2, holds |X1 ∪ X2| = |X1 | + |X2| - |X1 ∩ X2|.

Let's try to solve a bit more complicated case, i.e. n = 3.

Example 12.5.2

Let X1 = {0, 1, 2, 3}, X2 = {0, 2, 3, 4, 5, 6, 7, 8}, X3 = {0, 6, 7, 8, 9}, see Figure 12.5.1b. If we simply add |X1 | + |X2| + |X3|, then in this sum elements 2 and 3 are counted two times, they both belong to X1 and X2 (we can make a similar observation for elements 6, 7 as well as 8). The element 0 occurs in all three sets, that is why we count it three times. Therefore |X1 ∪ X2 ∪ X3| = |{0,1,2,3}| + |{0,2,3,4,5,6,7,8}|+ |{0,6,7,8,9}| - |{0,2,3}|- |{0,6,7,8}| - |{0}| +|{0}| = 4 + 8 +5 - 3 - 4- 1 + 1 = 10.

Fig. 12.5.1 We count cardinality of  the union of sets.

Lemma 12.5.2

For any finite sets X1 , X2 , X3, 

|X1 ∪ X2 ∪ X3| = |X1 | + |X2| + |X3| - |X1 ∩ X2|- |X1 ∩ X3| -|X2 ∩ X3|+ |X1 ∩ X2 ∩ X3|.

Question 12.5.1 In the group of 8 persons exactly 4 know each of the three cities: London, Paris and Rome. There are two persons who have visited both Paris and London and there are two persons that have visited Paris and Rome, but only one person that knows Rome and London. How many persons have been to all three places?

The formula in the lemma 12.5.2 can be generalized on any number of finite sets. The theorem 12.5.3  presented below is usually called the inclusion-exclusion principle.

Theorem 12.5.1

For any finite sets X1 , X2 , ..., Xn,

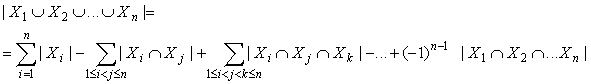
A proof of this theorem can be done by an induction on a number of sets (parameter n), but we do not present it this time. Now let's try to estimate the number of elements appearing in the introduced sum. Successive subsums include:

  1. n elements, i.e. ,
  2. as many elements as the number of 2-element subsets over set {1,2,...n}, i.e. ,
  3. as many elements as the number of 3-element subsets over set {1,2,...n}, i.e. , etc.

Summing up all, we obtain

It is quite unexpected that the inclusion-exclusion principle helps us to solve the problem of counting the number of surjections (see the previous subsection).

Theorem 12.5.2

If |X| = m and |Y| = n, then the number of all total functions form X onto Y amounts to

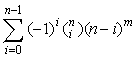
Proof.

Let Y = {1, ..., n} and Ai = {f : X → Y such that, i ∉ f(X)}. Ai be a family of functions which do not take the number i as the value, therefore they are not "onto Y" functions.

The number of all functions of the type f : X → Y is equal to n m. The number of all "not onto Y" functions is equal to the cardinality of set A1 ∪ ... ∪ An. To calculate |A1 ∪ ... ∪ An| we apply inclusion-exclusion principle:

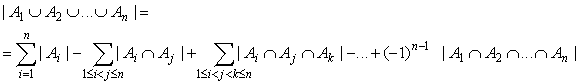
Every set Ai is a family  of functions from an m-element set into an (n-1)-element set, therefore |Ai| = (n-1)m. Set Ai ∩ Aj includes all functions which do not own values i and j in their ranges. These functions are assignments from the m-element set into the (n-2)-element set Y - {i, j}. We can derive all other cases using analogous reasoning, it leads to the following equality :


Finally, to count the number of surjections from X onto Y it will suffice to  subtract from the number of all functions these which are not onto Y.

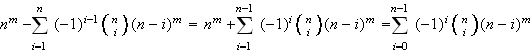
Problem  Using lemma 12.5.1 and the union's associativity property, prove the lemma 12.5.2.

Question 12.5.2 There are five differently addressed envelopes and five letters. You randomly put letters into envelopes. Find the number of possible situations in which no letter is in the proper envelope.


« previous section  « next section