Everyone knows that if we have 10 objects and just 4 boxes, then, after any distribution of these object into the mentioned boxes, at least one of them stores more than one object. Even if we use just 9 boxes this observation is still correct. The observation was first formulated by P. Dirichlet but is also known as the "pigeonhole principle". If we are given n boxes and m > n objects, at least one box must contain more than one object. Now, we generalize this fact in the following lemma 12.6.1.

Fig. 12.6.1 Dirichlet's box principle: given n boxes and m > n objects, at least one box must contain more than one object.

Justification.

If every subset obtained as a result of dividing X, includes less than |X|/n elements, then the cardinality of their union would  not be equal to |X|. ♦

Example 12.6.1

Assume that some 9 people P1, ..., P9 have a total weight equal to 810 kg. Can every three of these people get in a lift with the 250 kg capacity limit?

Solution. Let's consider the following matrix:

The total sum of weights in every row amounts to 810 kg., it is 2430 kg altogether. The matrix's columns produce 9 different triples. According to the Dirichlet's box principle at least one column sums up to 2430/9=270 kg. Therefore there exists (at least one) triple of people who cannot use the mentioned lift together.

The following theorem is a bit different version of the Dirichlet's box principle:

Question 12.6.1 In a set of selected 100 students every surname starts with the letters K, M, S or T. Explain why in this group there are at least 25 students whose names start on the same letter.

Example 12.6.2

Some University employs 5 professors who work in 4 different research disciplines (every professor represents exacly one discipline). It is expected that at the end of the academic year 40 students are going to defend their Master Thesis. According to the University regulations, every examination committee should be combined of 3 professors working on different disciplines. Prove that at least one committee must take part in 6 or more master thesis' examinaions.

Solution. Denote professors working on the same discipline as A and B. All boards can be split into 3 categories:

1. such that A and B are not present,
2. such that A is present and B not present,
3. such that A is not present and B is present.

There is only one board of category 1 and three boards of category 2 and 3 (we choose two remaining commitee members  from three professors, i.e. 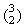). Thus the University can establish 7 different examination commitees. Now we define a function f which ascribes every student to some commitee. Because 40 > 5*7 thus, according to the Dirichlet's box principle for at least one x an inverse image f ^-1({x}) has more than 5 elements. It means that at least one examination commitee  must take part in 6 or more master thesis' defends.

Example 12.6.3

Let's assume that every student group is filled up with at most 15 students. A student can belong only to one group and all groups have pair-different symbols. There is an anonymous poll among 100 randomly chosen students (the aim of this poll is to evaluate the teaching staff). A poll is valid if and only if every student writes down on a poll's form his student's group symbol. After the poll's time ends it turns out that all poll's forms are valid and that the chosen students belong to 6 different groups. Prove that at least one of the students is untruthful.

Solution. According to the introduced assumptions there are at most 6*15 = 90 < 100 students in six students' groups. Thus, at least one symbol of group is checked on more than 15 poll's forms. At least 10 students are untruthful (probably this poll should be repeated).

Example 12.6.4

Let A be an arbitrary subset of power 10 of the set {1, 2, ..., 50}. Prove that A includes two different 5-element subsets such, that arithmetic sums over their elements are equal.

Solution. Let X be a set of all possible 5-element subsets of the set A. Of course, X has 252 elements. We define a function f : X → {1,2...50} such that for every 5-element set {a,b,c,d,e} holds

    f({a,b,c,d,e}) = a+b+c+d+e.

The function's f image is compounded with of 226 elements,  as 15 ≤ f({a,b,c,d,e}) ≤ 240. Therefore, using the theorem 12.6.2 there exist at least two arguments for which the function f takes the same value, and therefore there exist at least two subsets of A such that the sum of their elements are equal.

Question 12.6.2 Consider a chess board without two of the diagonally opposite corners. Is it possible to cover such a chess board with pieces of domino the size of which correspond exactly to two board squares?

« previous section

« next section