Przetwarzanie obrazów

Dziedziną pokrewną do grafiki komputerowej jest przetwarzanie obrazów. Niejednokrotnie, utworzone obrazy poddawane są dodatkowemu przetwarzaniu w celu uzyskania efektów, trudnych do zrealizowania bezpośrednio metodami grafiki komputerowej. W wykładzie poznamy wybrane metody z zakresu przetwarzania obrazów.

W przetwarzaniu obrazów punktem wyjścia jest istniejący obraz źródłowy w postaci mapy bitowej. Celem jest uzyskanie innej wersji tego obrazu, z jakichś względów lepszej z punktu widzenia użytkownika. Znanych jest wiele różnych metod przetwarzania obrazów. Ogólnie można wyróżnić wśród nich kilka podstawowych grup. Są to: przekształcenia geometryczne, przekształcenia punktowe, przekształcenia z wykorzystaniem filtrów, przekształcenia widmowe, przekształcenia morfologiczne. Tutaj ograniczymy się do scharakteryzowania trzech pierwszych grup.

Przekształcenia geometryczne dotyczą z reguły całych obrazów. Typowe przekształcenia to przesunięcia, obroty, odbicia. Zaliczymy tu również operacje kadrowania pozwalające wybierać z obrazu wybrany fragment. Na rysunku X.1 pokazano przykłady działania takich operacji. Często, operacje mogą być wykonywane w odniesieniu do wybranych fragmentów obrazu. Do wskazywania odpowiednich fragmentów służą różnego rodzaju maski.

Rys. X.1. Przykłady operacji na całej mapie bitowej. a) Oryginał, b) obrót o 90°, c) odbijanie w poziomie, d) pochylanie w kierunku osi x, e) obrót o kąt α, f) kadrowanie

Niektóre z operacji wykonywanych w odniesieniu do całego obrazu (bądź wybranego fragmentu) są łatwe algorytmicznie, inne są bardziej skomplikowane. Proponuję zastanowić się chwilę nad realizacją operacji obracania obrazu o 90° przeciwnie do ruchu wskazówek zegara, tak jak na rysunku X.1b. Można chyba zauważyć, że operacja taka może być zrealizowana w następujący sposób: zamieniamy kolejność pikseli w każdym wierszu a następnie zamieniamy miejscami wiersze i kolumny (por. rysunek X.2).

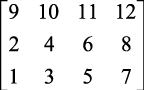
Rys. X.2. Obrót macierzy pikseli o 90° przeciwnie do kierunku ruchu wskazówek zegara

Obrót mapy bitowej o inny kąt niż 90° albo 180° jest operacją bardziej złożoną. Ogólną procedurę ilustruje rysunek X.3. Najpierw dokonujemy obrotu matrycy pikseli o zadany kąt. Następnie określamy docelową siatkę pikseli i dla każdego docelowego piksela znajdujemy te piksele pierwotnej matrycy, które są pokryte przez rozpatrywany piksel docelowy. Z kolei wyznaczamy stopień pokrycia każdego przykrytego piksela. Ten stopień pokrycia określa z jaką wagą należy wziąć intensywność przykrytego piksela przy obliczaniu wypadkowej barwy docelowego piksela.

Rys. X.3. Obrót mapy bitowej o kąt α

Zwróćmy uwagę na to, że przy przekształceniach tego typu, jak na przykład obroty mapy bitowej, musimy wykonać operacje w odniesieniu do poszczególnych pikseli obrazu początkowego, podczas gdy w przypadku opisu wektorowego obrazu dokonywaliśmy przekształceń w odniesieniu do poszczególnych obiektów, a w szczególności do wierzchołków obiektów bądź punktów sterujących.

Przekształcenia punktowe obejmują operacje dotyczące poszczególnych pikseli obrazu niezależnie od stanu pikseli sąsiednich. Przykłady takich operacji to tworzenie negatywu obrazu, zmiana obrazu przy wykorzystaniu odpowiedniej charakterystyki przejściowej, progowanie (binaryzacja), pseudokolorowanie. Przykłady działania operacji pokazano na rysunku X.4.

Rys. X.4. Przykłady ilustrujące działanie wybranych operacji jednopunktowych: (a) oryginał, (b) negatyw, (c) progowanie, (d) pseudokolorowanie, (e) zamiana poziomów jasności, (f) charakterystyka przejściowa

Przy przetwarzaniu jednopunktowym wykonuje się pewną operację w odniesieniu do każdego piksela niezależnie. Sposób wykonania operacji na ogół opisuje się albo poprzez podanie tablicy przekodowania wartości poszczególnych pikseli albo poprzez określenie funkcji przypisującej nowe wartości pikselom o określonych jasnościach.

Tablica przekodowania jest stosowana na przykład przy operacjach zmieniania barw w obrazie. Każdy element takiej tablicy określa nową barwę jaką należy zastąpić określoną barwę w oryginalnym obrazie. Na przykład, pikselowi o odcieniu szarości 12 należy przypisać barwę zieloną, a pikselowi o odcieniu szarości 127 należy przypisać barwę czerwoną itd. Tego typu przetwarzanie obrazu jest określane jako pseudokolorowanie. Tablica zmiany wartości pikseli może w szczególności określać wyłącznie wymianę wartości poszczególnych pikseli w ramach pierwotnego zbioru wartości pikseli występujących w obrazie. Tego typu operację wykonano na rysunku X.4d.

Wymagany rodzaj przekształcenia można określać za pomocą funkcji przypisujących nowe wartości poszczególnym wartościom oryginalnym. Na przykład w celu uzyskania negatywu obrazu z odcieniami szarości można wykorzystać funkcję typu L’ = 255 - L, gdzie jasności pikseli: pierwotna L i nowa L’ są zapisane dwójkowo w skali od 0 do 255. Stosowane mogą być różne funkcje: potęgowe, wykładnicze, logarytmiczne, monotoniczne i niemonotoniczne, bądź dobrane indywidualnie dla potrzeb konkretnego zadania przetwarzania. Na przykład obrazek z rysunek X.4f został uzyskany z obrazka z rysunku X.4a za pomocą funkcji takiej jak na rysunku X.5a. W szczególnym przypadku funkcja może być taka jak na rysunku X.5b. Wtedy wszystkie poziomy jasności mniejsze od wartości progowej, przy której następuje zmiana poziomu funkcji zostają zamienione na barwę czarną, a wszystkie poziomy o wartości większej od wartości progowej są zamieniane na barwę białą. W takim przypadku uzyskujemy obraz czaro-biały a wykonywane przekształcenie jest określane jako progowanie obrazu (por. rysunek X.4c).

Rys. X.5. Przykłady funkcji określających sposób zmiany jasności pikseli. Na osi poziomej są wartości jasności przed przekształceniem, na osi pionowej wartości jasności pikseli po przekształceniu. a) Funkcja wykorzystana do uzyskania obrazu z rysunku X.4f, b) funkcja progowa

Kolejną grupę przekształceń tworzą przekształcenia wykorzystujące sąsiedztwo pikseli. Operacje tego typu wykonuje się stosując odpowiednie filtry czy też maski. Operację wykonuje się w odniesieniu do każdego piksela pierwotnego obrazu. Wynik operacji zapisuje się w nowym docelowym obrazie. Istotę operacji wyjaśnia rysunek X.6.

Rys. X.6. Ilustracja metody przetwarzania z wykorzystaniem filtru 3 × 3. Na podstawie informacji o pikselach tworzących sąsiedztwo danego piksela wyznaczana jest jasność piksela w docelowym obrazie

Maska (filtr) jest to tablica elementów, najczęściej kwadratowa o wymiarach 3 × 3, 5 × 5 itp. Poszczególne elementy tablicy stanowią współczynniki wagowe, przez które mnoży się odpowiednie wartości pikseli z sąsiedztwa analizowanego piksela. Wartość nowego piksela wyznacza się z zależności

$$p_(x,y)={∑↙{i,j=-m}↖m w_{ij}\;p_{x+i,y+j}}/{∑↙{i,j=-m}↖m w_{ij}}$$

gdzie współczynniki $w_{ij}$ są elementami filtru kwadratowego o boku $2m + 1$, $p_{x,y}$ jest przetwarzanym pikselem, natomiast $p_{x+i,y+i}$ są pikselami sąsiedztwa w kwadracie o boku $2m + 1$. Jeżeli suma współczynników wagowych filtru jest równa 0 albo 1, to wynikową wartość piksela określa się z zależności

$$p_(x,y)=∑↙{i,j=-m}↖m w_{ij}\;p_{x+i,y+j}$$

Zauważmy dodatkowo, że nieco odmiennie muszą być potraktowane piksele należące do pierwszego i ostatniego wiersza obrazu. Stosuje się tu różne rozwiązania. W najprostszym przypadku nie przetwarza się pikseli należących do tych wierszy. W bardziej złożonym rozwiązaniu stosuje się specjalne filtry o wymiarze 2 × 3.

Rodzaj wykonywanej operacji zależy od używanej maski. Znanych jest wiele różnych filtrów. W szczególności wyróżnia się filtry dolnoprzepustowe, które pozwalają usuwać drobne zakłócenia w obrazie (uśredniać, co w efekcie prowadzi do pewnego rozmycia obrazu), górnoprzepustowe, które pozwalają uwypuklać krawędzie występujące w obrazie (wyostrzać obraz) oraz filtry wykrywające krawędzie. Na rysunku X.7 podano kilka przykładowych filtrów. Natomiast na rysunku X.8 pokazano kilka przykładów stosowania takich operacji.

Rys. X.8. Przykłady stosowania filtrów: a) oryginał, b) filtr dolnoprzepustowy, c) filtr górnoprzepustowy, d) wykrywanie krawędzi

W przetwarzaniu obrazów wykorzystuje się pojęcie histogramu obrazu. Histogram jest to wykres, w którym dla każdej barwy (odcienia szarości) występującej w obrazie podaje się liczbę pikseli o tej barwie znajdujących się w obrazie. Liczby te są reprezentowane za pomocą pionowych odcinków o odpowiednich wysokościach. Na rysunkach X.9a i b pokazano przykładowy obraz i jego histogramy, odpowiednio dla składowych R, G i B.

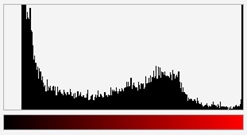
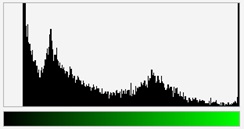
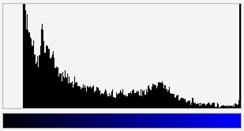
Rys. X.9. a) Obraz i b) jego histogramy dla barw RGB

Na zakończenie zwróćmy uwagę, że w przetwarzaniu obrazów wykorzystuje się kilka obrazów wzorcowych, które są wykorzystywane do weryfikacji działania różnych algorytmów. Jednym z takich obrazów jest tzw. obraz Leny, w oryginale kolorowy, oraz w odcieniach szarości (rys. X.10). Obraz ten zostanie dalej wykorzystany do pokazania kilku dalszych operacji przetwarzania obrazów.

Rys. X.10. Wzorcowy obraz Leny

Na rys. X.11 pokazano kilka wersji obrazu Leny. Na rysunku a) pokazano obraz z gamma korekcją o wartości 2,2. Korekcja taka jest stosowana w celu kompensacji zniekształceń wnoszonych przez nieliniową charakterystykę monitorów. Na rysunku b) pokazany jest efekt posteryzacji, który powstaje wtedy gdy liczba dostępnych odcieni szarości staje się zbyt mała. Na rysunku c) pokazana jest zaszumiona wersja obrazu. Na rysunku d) pokazany jest efekt wykrywania krawędzi w obrazie.

Rys. X.11. Przykładowe modyfikacje obrazu. a). Korekcja gamma, b) posteryzacja, c) Dodanie szumu do obrazu, d) wykrycie krawędzi w obrazie

Na rysunku X.12 pokazano cztery przykłady efektów zniekształcania obrazu.

Rys. X.12. Przykłady zniekształcania obrazu

Na rysunku X.13 pokazano dwa przykłady modyfikowania obrazu poprzez wstawianie innych obrazów

Rys. X.13. Przykłady modyfikacji treści obrazu

Profesjonalne programy do przetwarzania obrazów oferują mnóstwo innych operacji na obrazach cyfrowych.