Algorytmy grafiki 2D

Grafika 2D

W grafice 2D, przy tworzeniu obrazu na płaszczyźnie, operuje się obiektami takimi jak odcinki, figury czy krzywe. Obiekty te opisywane są za pomocą wierzchołków bądź punktów sterujących i odpowiednich atrybutów. Problem rasteryzacji obiektów (omówiony w poprzednim wykładzie), czyli wyznaczania wszystkich pikseli obiektów, jest odkładany do ostatniej fazy tworzenia obrazu.

W odniesieniu do poszczególnych obrazów opisanych wektorowo, wykonuje się różne operacje. Cechą charakterystyczną tych operacji jest to, że są one wykonywane w odniesieniu do wierzchołków obiektów bądź punktów sterujących istotnych dla opisu tych obiektów. Same obiekty są odtwarzane dopiero na podstawie punktów uzyskanych w wyniku wykonania operacji. Najczęstszą grupę operacji wykonywanych w stosunku do obiektów stanowią przekształcenia geometryczne: przesunięcia (translacje), obroty, skalowanie i pochylanie.

Przekształcenia geometryczne

Przekształcenie polegające na przesunięciu (translacji) obiektu polega na zmianie położenia wszystkich jego wierzchołków o zadany wektor przesunięcia. Przykład takiego przekształcenia pokazano na rysunku V.1. Na rysunku podano również równania wykorzystywane przy takim przekształceniu. Równanie te pozwalają znaleźć współrzędne $(x’,y’)$ punktu po przesunięciu o wektor $T(T_x,T_y)$.

$x'=x+T_x$
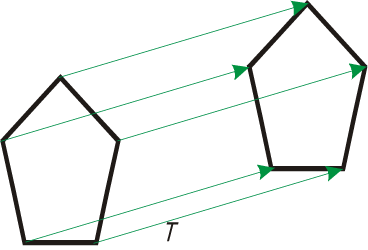
$y'=y+T_y$

Rys. V.1. Przesunięcie obiektu o wektor T 

Skalowanie pozwala zmienić wielkość obiektu ze współczynnikiem skalowania S. Przykład skalowania pokazano na rysunku V.2. Obok pokazano równania umożliwiające znalezienie nowego położenia punktu poddanego skalowaniu względem osi x ze współczynnikiem $S_x$ i względem osi y ze współczynnikiem $S_y$.

$x'=x·S_x$
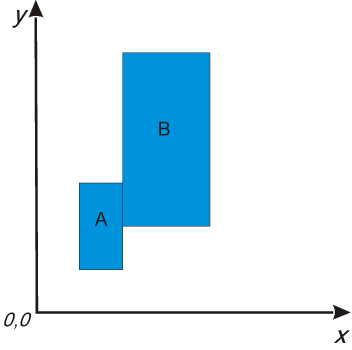
$y'=y·S_y$

Rys. V.2. Przykład skalowania obiektu ze współczynnikami skalowania $S_x=S_y=2$. Punktem odniesienia jest początek układu współrzędnych

Zauważmy, że przy operacji skalowania istotny jest punkt odniesienia. Na rysunku V.2 punktem odniesienia jest początek układu współrzędnych. Ogólnie, punkt odniesienia $x_f$, $y_f$ dla skalowania może być w dowolnym miejscu na płaszczyźnie. Na rysunku V.3 pokazano przykład skalowania, w którym punkt odniesienia znajduje się w lewym dolnym rogu skalowanego obiektu.

$x'=x·S_x+x_f(1-S_x)$
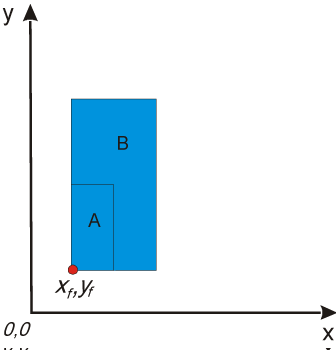
$y'=y·S_y+y_f(1-S_y)$

Rys. V.3. Przykład skalowania obiektu ze współczynnikami skalowania $S_x=S_y=2$. Punktem odniesienia jest punkt o współrzędnych $x_f$ = 1, $y_f$ = 1

Na rysunku V.4 pokazano przykład obrotu obiektu wokół początku układu współrzędnych o kąt θ. (Obrót o kąt dodatni jest w kierunku przeciwnym do ruchu wskazówek zegara). Podano również równania umożliwiające obliczanie współrzędnych punktów po obrocie o zadany kąt θ względem początku układu współrzędnych.

$x'=x\cosθ-y\sinθ$
$y'=x\sinθ+y\cosθ$

Rys. V.4. Obrót obiektu o zadany kąt θ wokół początku układu współrzędnych

Podobnie jak w przypadku skalowania, dla obrotu (rotacji) istotny jest punkt o współrzędnych $x_r$, $y_r$, wokół którego następuje obrót. Ogólnie, może to być dowolny punkt na płaszczyźnie. Na rysunku V.5 pokazano przykład obrotu tej samej figury co poprzednio, o taki sam kąt, ale wokół innego, przykładowego, punktu obrotu.

$x'=x_r+(x-x_r)\cosθ-(y-y_r)\sinθ$
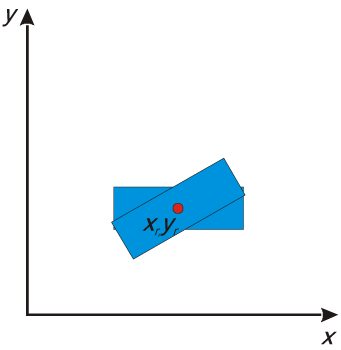
$y'=y_r+(x-x_r)\sinθ+(y-y_r)\cosθ$

Rys. V.5. Obrót obiektu o zadany kąt θ wokół punktu o współrzędnych $x_r$, $y_r$

Kolejne przydatne w praktyce przekształcenie, to pochylenie wzdłuż osi x ze współczynnikiem a albo wzdłuż osi y ze współczynnikiem b. Oba rodzaje pochyleń są pokazane na rysunku V.6, wraz z odpowiednimi równaniami.

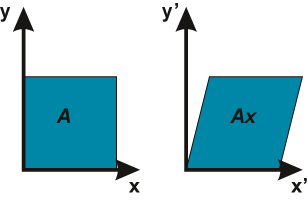
Rys. V.6. Pochylanie obiektu wzdłuż osi x (Ax) i wzdłuż osi y (Ay)

Współrzędne jednorodne

W grafice komputerowej, omówione wyżej przekształcenia geometryczne, są realizowane z wykorzystaniem tak zwanych współrzędnych jednorodnych.

Obiekt opisany w określonym układzie współrzędnych prostokątnych, na przykład x,y, może być przedstawiony również w układzie współrzędnych o jeden wymiar większym, na przykład w układzie x, y, z. Wtedy, na przykład w przypadku punktu o współrzędnych (a,b) dochodzi jedna współrzędna, która w ogólnym przypadku może mieć dowolną wartość. Jeżeli przyjmie się, że ta nowa współrzędna będzie miała wartość 1 to mówimy, że punkt jest reprezentowany we współrzędnych jednorodnych znormalizowanych. I tak, punkt o współrzędnych (a,b) ma teraz współrzędne (a,b,1). Dodajmy od razu, że gdyby zdarzyło się, że w wyniku obliczeń we współrzędnych jednorodnych otrzymalibyśmy współrzędne (a’,b’,w), to od razu trzeba wykonać krok normalizacyjny tak, żeby uzyskać postać standardową dla której w = 1. Oznacza to że wszystkie współrzędne punku trzeba podzielić przez w.

Przejście do współrzędnych jednorodnych umożliwia uzyskanie jednolitego zapisu podstawowych przekształceń geometrycznych: przesunięcia, obrotu, skalowania i innych - zwłaszcza istotne jest tu uwzględnienie operacji przesunięcia. Ułatwia to w konsekwencji realizację sprzętowego wspomagania obliczeń i w efekcie przyspieszanie obliczeń.

Przy tym podejściu wszystkie operację są realizowane w postaci mnożenia wektora kolumnowego reprezentującego przekształcany punkt (x,y,1) przez macierz 3 x 3 z współczynnikami odpowiednimi dla wykonywanego przekształcenia. W wyniku uzyskuje się współrzędne punktu po przekształceniu (x’,y’,1)

Macierze dla poszczególnych przekształceń geometrycznych na płaszczyźnie wyglądają następująco.

Przesunięcie o wektor (T_x, T_y)

Skalowanie ze współczynnikami skalowania S_x, S_y

Obrót o kąt θ względem początku układu współrzędnych

Pochylanie wzdłuż osi x ze współczynnikiem a i wzdłuż osi y ze współczynnikiem b

Jedną z zalet reprezentowania przekształceń w postaci macierzowej jest to, że macierze poszczególnych przekształceń można mnożyć przez siebie w celu uzyskania macierzy dla przekształcenia złożonego. Jeżeli więc konieczne będzie wykonanie szeregu przekształceń w odniesieniu do określonego punktu P, to można wstępnie wykonać mnożenie macierzy $M_i$ kolejnych przekształceń (w ustalonej kolejności) i uzyskać jedną macierz wypadkową M’ dla tego ciągu przekształceń. Jest to szczególnie korzystne obliczeniowo wtedy, gdy ten sam ciąg przekształceń ma być wykonany w odniesieniu do wielu punktów. Wyjaśniają to poniższe równania.

$P'=M_3M_2M_1P$
$M’=M_3M_2M_1$
$P’=M’P$.

Jeżeli na przykład chcielibyśmy obracać obiekt nie względem początku układu współrzędnych a względem pewnego punktu P(x₁,x₂), to powinniśmy wykonać kolejno następujące operacje: takie przesunięcie obiektu, żeby punkt P(x₁,x₂) znalazł się w początku układu współrzędnych, wykonanie obrotu o kąt θ, takie przesunięcie obróconego obiektu żeby punkt znajdujący się w początku układu współrzędnych wrócił do początkowego położenia P(x₁,x₂). Oznacza to, że kolejno powinniśmy wykonać operacje przesunięcia o wektor (-x₁,-x₂), obrotu o kąt θ i przesunięcia o wektor (x₁,x₂). Można to zrealizować wykonując kolejno trzy operacje mnożenia wektora przez odpowiednie macierze. Równoważny sposób polega na tym, że na początku znajdujemy macierz wypadkową dla całej operacji, a dopiero potem korzystamy z niej w odniesieniu do poszczególnych wierzchołków obracanego obiektu. Niżej pokazany jest proces wyznaczania wypadkowej macierzy. Zwróćmy uwagę na kolejność zapisu macierzy (od prawej strony do lewej zgodnie z kolejnością wykonywanych przekształceń). Przypomnijmy również, że w ogólnym przypadku mnożenie macierzy nie jest przemienne.

W podobny sposób można wyznaczać macierze wypadkowe dla innych złożonych przekształceń. Proponuję samodzielne znalezienie macierzy wypadkowej dla operacji skalowania względem punktu innego niż początek układu współrzędnych.

Obcinanie

Operacja obcinania może być potrzebna wtedy, gdy zaprojektowany rysunek jest na tyle duży, że nie może być w całości wyświetlony na ekranie. W takiej sytuacji sensowne jest wybranie z rysunku tylko tego fragmentu, który może pojawić się na ekranie i poddać przetwarzaniu tylko te obiekty, które znajdą się w wybranym fragmencie (oknie) w całości lub częściowo. Znanych jest kilka różnych metod obcinania. Tutaj ograniczymy się do omówienia klasycznej metody Cohena-Sutherlanda obcinania odcinków oraz metody Sutherlanda-Hodgmana obcinania wielokątów.

Zacznijmy od problemu obcinania odcinków. Algorytm jest realizowany w dwóch fazach. W pierwszej fazie chodzi o to, żeby z procesu obcinania wyeliminować te odcinki, które z pewnością nie wymagają obcinania: albo leżą poza oknem albo całkowicie mieszczą się w oknie. Przykłady różnego usytuowania odcinków względem okna pokazuje rysunek V.7. W drugiej fazie każdy odcinek spośród tych, które pozostaną po pierwszej fazie, jest niezależnie obcinany.

Rys. V.7. Przykładowe położenia odcinków względem okna obcinania

Dla celów szybkiego sprawdzania, czy odcinek może być wyeliminowany z dalszej procedury obcinania Cohen i Sutherland zaproponowali żeby podzielić płaszczyznę okna na dziewięć części uzyskanych w wyniku przedłużenia krawędzi okna. Każdej części został przypisany kod czterobitowy. Ilustruje to rysunek V.8. Zasada przypisania kodów jest następująca. Wszystkie części leżące z lewej strony okna mają jedynkę na pierwszej pozycji kodu. Wszystkie części leżące z prawej strony okna mają jedynkę na drugiej pozycji kodu itd.

Rys. V.8. a) Podział obszaru na części i sposób przypisania kodów, b) przykładowe analizowane odcinki

Decyzję co do możliwości wyeliminowania odcinka podejmuje się w następujący sposób. Każdemu końcowi odcinka przypisywany jest kod obszaru, w którym ten koniec znajduje się. Następnie znajduje się iloczyn logiczny tych kodów (niezależnie wyznacza się iloczyn logiczny dla każdej pary odpowiadających sobie bitów). Jeżeli iloczyn jest różny od zera, to odcinek można odrzucić (na przykład odcinek A na rysunku) jako leżący poza oknem. Można również wyeliminować z dalszej procedury obcinania odcinki, których oba końce leżą w oknie (odcinek D na rysunku). Innych odcinków nie można wyeliminować, nawet mimo tego, że z pewnością leżą poza oknem, tak jak na przykład odcinek B na rysunku. Wynika to stąd, że tak prosta procedura nie może rozróżnić odcinków takich jak B i C na rysunku. Niemniej, mimo, że skuteczność procedury nie jest stuprocentowa, jest ona stosowana ze względu na prostotę. Wszystkie odcinki, które nie zostaną wyeliminowane są poddawane dalszej procedurze obcinania.

Procedura obcinania składa się z czterech kroków. W każdym z nich dokonuje się obcięcia przez prostą na której leży jedna z krawędzi okna, zawsze w ustalonej kolejności. W kroku obcinania przez wybraną prostą znajduje się przecięcie odcinka z tą prostą i usuwa się tę część odcinka, która leży na zewnątrz okna. Procedurę ilustruje rysunek V.9.

Rys. V.9. Procedura obcinania odcinka przez kolejne proste wyznaczane przez krawędzie okna

Procedurę obcinania wielokątów wypukłych można zrealizować następująco. Najpierw warto sprawdzić jak wielokąt jest położony względem okna. Możliwe przypadki są pokazane na rysunku V.10.

Rys. V.10. Możliwe położenia wielokąta względem okna. a) Obiekty są rozłączne, b) wielokąt leży wewnątrz okna, c) wielokąt przecina się z oknem, d) okno zawiera się w wielokącie

W trzech przypadkach sposób postępowania jest oczywisty. Jedynie w przypadku c) konieczne jest kontynuowanie procedury. Można ją zrealizować w czterech krokach. W każdym kroku można dokonywać obcinania przez kolejną krawędź okna (a ściślej przez prostą, na której leży krawędź). Za każdym razem odrzucana jest część wielokąta leżąca po zewnętrznej stronie okna. Ilustruje to rysunek V.11. W tym przypadku wystarczyło obcięcie przez dwie krawędzie okna.

Rys. V.11. Przykład obcinania wielokąta

W procedurze, w najprostszym przypadku, można bezpośrednio wykorzystać algorytm obcinania odcinków w odniesieniu do poszczególnych krawędzi obcinanego wielokąta. Wygodniejsze może się jednak okazać skorzystanie z pomysłu zaproponowanego przez Sutherlanda i Hodgmana.

Załóżmy, że będziemy przeglądali krawędzie wielokąta w kierunku przeciwnym do ruchu wskazówek zegara. Załóżmy też, że dla każdej prostej, na której leży krawędź okna wyróżniamy stronę zewnętrzną i wewnętrzną - po stronie wewnętrznej leży okno. Istotę pomysłu ilustruje rysunek V.12. Wyróżniono na nim cztery sytuacje jakie mogą wystąpić przy analizie relacji krawędzi wielokąta z rozpatrywaną prostą. Krawędź wielokąta może przechodzić ze strony zewnętrznej na stronę wewnętrzną rozpatrywanej prostej. Wtedy znajdujemy punkt przecięcia P i na pomocniczą listę wpisujemy ten punkt przecięcia P oraz docelowy koniec krawędzi wielokąta W. Jeżeli krawędź wielokąta leży całkowicie po wewnętrznej stronie rozpatrywanej prostej, to na pomocniczą listę wpisujemy docelowy wierzchołek krawędzi wielokąta W. Jeżeli krawędź wielokąta przechodzi na stronę zewnętrzną rozpatrywanej prostej, to na pomocniczą listę wpisujemy punkt przecięcia z krawędzią okna. Jeżeli krawędź wielokąta leży w całości po stronie zewnętrznej rozpatrywanej prostej, to nic nie wprowadzamy na pomocniczą listę.

Rys. V.12. Cztery przypadki usytuowania krawędzi wielokąta względem rozpatrywanej prostej. Dla każdego przypadku zaznaczono informacje jakie należy wprowadzić na pomocniczą listę

Na rysunku V.13 pokazano poprzedni przykład obcinania wielokąta przez okno z uwzględnieniem przedstawionych reguł. Dla uproszczenia, zamiast tworzyć pomocniczą listę, bezpośrednio na rysunku zaznaczono odpowiednie punkty, przypisując im numery w kolejności pojawiania się. W każdym kroku analizę zaczynano od krawędzi oznaczonej literą A. Każdorazowo, po ustaleniu pomocniczej listy, łączy się punkty w kolejności pojawiania się na liście: od pierwszego do ostatniego i do pierwszego. Pozostawia się powstały wielokąt.

Rys. V.13. Kolejne kroki algorytmu obcinania

Proponuję samodzielnie wykorzystać algorytm obcinania dla wielokąta pokazanego na rysunku V.14.

Rys. V.14. Przykład do samodzielnego wykonania obcinania

Krzywe w grafice komputerowej

Krzywe wykorzystywane w grafice komputerowej są reprezentowane jako:

W grafice spotyka się krzywe o różnych właściwościach: globalnych albo lokalnych.

W kontekście właściwości globalnych można mówić o krzywych zamkniętych, krzywych z przecięciami, krzywych złożonych z segmentów (rys. V.15a), krzywych interpolujących punkty (przechodzących przez zadany zbiór punktów) (rys. V.15b), krzywe aproksymujące punkty (przybliżające zadany zbiór punktów) (rys. V.15c)

Rys. V.15. Przykładowe krzywe. a) Krzywa złożona z segmentów, b) krzywa interpolująca punkty, c) krzywa aproksymująca punkty

Wśród właściwości lokalnych krzywych wyróżnia się przede wszystkim parametry opisujące ciągłość w punktach styczności segmentów krzywej.

Przy podejściu analitycznym wykorzystuje się pojęcie ciągłości parametrycznej $C^n$ dla której wszystkie pochodne do n włącznie są takie same z obu stron punktu styczności segmentów (np. dla ciągłości $C^1$ zachodzi równość $f_1^'(1)=f_2^'(0)$, gdzie wartość 1 bieżącego parametru odpowiada końcowi jednego segmentu a wartość 0 początkowi drugiego segmentu).

W kontekście grafiki komputerowej wykorzystuje się najczęściej pojęcie ciągłości geometrycznej. Ciągłość geometryczna $G^o$ oznacza, że dwie krzywe mają jedynie wspólny punkt. Ciągłość $G^1$ oznacza, że w wspólnym punkcie styczne do krzywych są współliniowe. Ciągłość $G^2$ oznacza, że dwie krzywe ciągłe według kryterium $G^1$, mają takie same krzywizny w wspólnym punkcie (rys. V.16).

Rys. V.16. Ilustracja ciągłości geometrycznych

Inne właściwości lokalne krzywej, to na przykład: położenie punktu na krzywej, kierunek przesuwania się punktu wzdłuż krzywej, miara przebytej odległości wzdłuż krzywej itd.

Ważną klasą krzywych są krzywe wielomianowe opisywane funkcją

$$f(t)=a_0+a_1t+a_2t^2+...+a_nt^n=∑↙{i=0}↖n a_it^i$$

Funkcję wielomianową można również zapisać w postaci

$$f(t)=∑↙{i=0}↖n c_ib_i(t)$$

gdzie $b_i(t)$ to wielomiany określane jako funkcje bazowe o postaci zależnej od rodzaju krzywej. Przy odpowiednim doborze funkcji bazowych współczynniki $c_i$ umożliwiają sterowanie kształtem krzywej. Przykładem tego typu krzywych są krzywe Béziera.

Krzywe Béziera

Krzywe Béziera są krzywymi wielomianowymi, których kształt można opisywać za pomocą tak zwanych punktów sterujących (kontrolnych).

Równania opisujące krzywe Béziera są zapisywane w postaci parametrycznej.

gdzie $P_k$ to punkty sterujące a $B_{k,n}(u)$, to funkcje bazowe (tak zwane wielomiany Bernsteina) związane z poszczególnymi punktami sterującymi

W ogólnym przypadku liczba punktów sterujących nie jest ograniczona - jednak im większa liczba tych punktów, tym wyższy stopień wielomianu opisującego krzywą. W praktyce najczęściej wykorzystuje się krzywe trzeciego stopnia definiowane za pomocą czterech punktów sterujących i dalej ograniczymy się do omówienia takich właśnie krzywych.

Na rysunku V.17 pokazano kilka przykładów krzywych Béziera zdefiniowanych za pomocą czterech punktów sterujących.

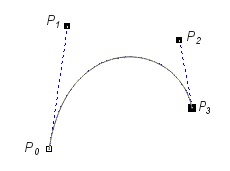
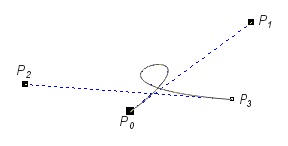
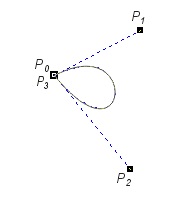
Rys. V.17. Przykładowe krzywe Béziera

Przyglądając się pokazanym przykładom można zauważyć kilka wspólnych cech charakterystycznych dla krzywych Béziera. Istotna jest kolejność punktów sterujących. Krzywa zawsze przechodzi przez punkty sterujące: pierwszy i ostatni. Odcinek łączący dwa pierwsze punkty sterującej jest zawsze styczny do krzywej w pierwszym punkcie sterującym. Podobnie, odcinek łączący dwa ostatnie punkty sterujące jest styczny do krzywej w ostatnim punkcie sterującym. Ponadto, warto również zwrócić uwagę na fakt, iż krzywa zawsze leży we wnętrzu wielokąta opisanego na całym zbiorze punktów sterujących. Możliwe jest również tworzenie krzywych zamkniętych. Zmiana położenia dowolnego punktu sterującego powoduje zmianę kształtu krzywej - właściwość ta umożliwia łatwą edycję krzywych.

Równanie dla krzywej trzeciego stopnia ma postać

$$P(u)=(1-u)^3P_0+3u(1-u)^2P_1+3u^2(1-u)P_2+u^3P_3$$

Występujący w równaniu parametr bieżący u zmienia się wzdłuż krzywej od wartości 0 na początku krzywej do wartości 1 na końcu krzywej. Punkty $P_k$, k = 0,1,2,3 są punktami sterującymi krzywej. Wykresy funkcji bazowych są pokazane na rysunku V.18. Warto zauważyć, że każda funkcja bazowa wpływa na kształt krzywej w całym zakresie zmian parametru u (w mniejszym lub większym stopniu).

Rys V.18. Funkcje bazowe dla krzywych Béziera definiowanych przez cztery punkty sterujące. Na osi poziomej wartość parametru u

Możliwe jest tworzenie bardziej złożonych krzywych Béziera za pomocą składania z segmentów. Przykład pokazano na rysunku V.19. Zwróćmy uwagę na ciągłość krzywej w punktach łączenia segmentów. Warunkiem uzyskania ciągłości jest to, żeby dwa końcowe punkty sterujące jednego segmentu (P_a2, P_a3 na rysunku) leżały na tej samej prostej co dwa pierwsze punkty sterujące drugiego segmentu (P_b0, P_b1 na rysunku), przy czym punkt ostatni P_a3 pierwszego segmentu pokrywa się z pierwszym punktem P_b0 drugiego segmentu.

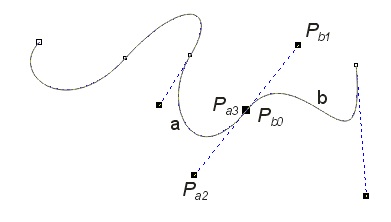
Rys. V.19. Przykład krzywej Béziera złożonej z czterech segmentów

Narzędzia w programach grafiki 2D

W wykładzie poznaliśmy kilka podstawowych algorytmów wykorzystywanych w grafice 2D. Algorytmy te są wykorzystywane w różnych programach graficznych. Każdy z takich programów udostępnia narzędzia ułatwiające tworzenie poszczególnych obiektów i całych obrazów. Zestawy dostępnych narzędzi są różne w różnych programach. W przypadku większości programów omówienie wszystkich narzędzi i sposobów ich stosowania jest opisywane w obszernych podręcznikach i w zasadzie wymaga bezpośredniego korzystania z danego programu.

W trakcie zajęć laboratoryjnych poznamy profesjonalny program graficzny CorelDraw Opis narzędzi tego programu można znaleźć w podręczniku do aktualnej wersji programu. Można oczywiście zawsze skorzystać z dostępnego w programie „Helpu”.