Cyfrowa reprezentacja obrazu

Obraz, podobnie jak każda inna informacja w komputerze, musi być przedstawiony w postaci cyfrowej. W wykładzie wyjaśniono sposób reprezentacji obrazu w postaci cyfrowej oraz omówiono problemy związane ze stosowaniem takiej reprezentacji.

W otaczającym nas świecie obserwujemy obrazy ciągłe składające się z nieskończenie wielu punktów, przy czym każdy punkt może być reprezentowany za pomocą nieskończenie wielu wartości. Każda próba cyfrowego reprezentowania takich obrazów oznacza konieczność ograniczenia zarówno liczby modelowanych punktów, poprzez próbkowanie obrazu, jak i liczby wartości jakie można przypisać poszczególnym punktom, poprzez kwantowanie rzeczywistego zakresu wartości.

Proces próbkowania obrazu można wyjaśnić poglądowo w następujący sposób. Wyobraźmy sobie, że na zdjęcie (przyjmujemy tu upraszczające założenie, że zdjęcie dobrej jakości odzwierciedla obraz rzeczywisty) nanosimy siatkę prostokątną (rys.II.1a) Każdy węzeł siatki odpowiada jednej próbce obrazu. Zbiór tak określonych próbek stanowi pewne przybliżenie obrazu, tym lepsze im liczba próbek jest większa.

Każda próbka obrazu ma pewną barwę Bpr, której w procesie kwantowania można przypisać najbliższą barwę Bpiks spośród dopuszczalnego zbioru barw, którego liczność określa długość słowa reprezentującego barwy w systemie graficznym (rys. II.1b). Cyfrowa reprezentacja próbki obrazu jest określana w grafice komputerowej jako piksel.

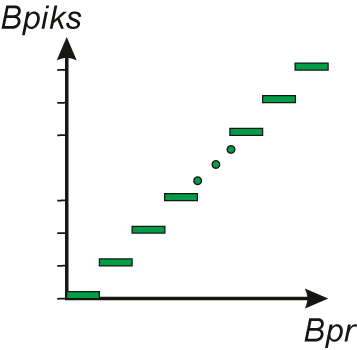
Rys. II.1. Ilustracja: a) procesu próbkowania obrazu, b) procesu kwantowania barwy próbki

O ile konwersja obrazów rzeczywistych na postać cyfrową wymaga próbkowania obrazu i kwantowaniu próbek, to konwersja odwrotna nie wymaga żadnych operacji. Następuje ona w czasie obserwacji przez człowieka wyświetlanego obrazu. Wykorzystuje się tu fakt, że system wzrokowy człowieka umożliwia odbieranie informacji dyskretnej, takiej jak obraz cyfrowy, jako informacji ciągłej (oczywiście przy dostatecznie dobrej wizualizacji obrazu).

Obok opisanej wyżej reprezentacji obrazu, w której próbki są identyfikowane z węzłami siatki, możliwa jest reprezentacja, w której próbki są identyfikowane z oczkami siatki. Wtedy, próbce jest przypisana barwa uśredniona w obrębie powierzchni oczka siatki.

Opisane sposoby reprezentacji cyfrowej rzeczywistego obrazu znajdują odzwierciedlenie w dwóch modelach reprezentacji obrazu cyfrowego: punktowym i powierzchniowym. Na rysunku II.2 pokazane są oba modele. Warto zaznaczyć, że oba modele stanowią przybliżony sposób reprezentowania pikseli wyświetlanych na monitorach, bowiem w rzeczywistości piksele ani nie są nieskończenie małe (tak jak w modelu punktowym) ani nie wypełniają powierzchni ekranu w sposób ciągły (tak jak to jest w modelu powierzchniowym). W praktyce wykorzystuje się oba modele, zależnie od wygody. Zwróćmy też uwagę na sposób określania współrzędnych pikseli w obu metodach. W metodzie punktowej są to numery wiersza i kolumny, opisujące węzeł siatki w którym znajduje się piksel. W modelu powierzchniowym są to współrzędne środka oczka siatki - oznacza to przesunięcie współrzędnych poszczególnych pikseli o ½ skoku siatki, względem współrzędnych modelu punktowego.

Rys. II.2 Dwie równoważne reprezentacje pikseli: a) punktowa, b) powierzchniowa

Zauważmy, że opisane wyżej operacje próbkowania i kwantowania obrazów rzeczywistych realizują na przykład aparaty cyfrowe, za pomocą których obrazy rzeczywiste są utrwalane w postaci obrazów cyfrowych. W grafice komputerowej obrazy cyfrowe, a dokładniej poszczególne piksele tych obrazów, są generowane za pomocą odpowiednich metod obliczeniowych.

Jeżeli z siatką prostokątną pikseli obrazu cyfrowego zwiążemy układ współrzędnych prostokątnych $x,y$, to położenie każdego piksela p można opisać podając odpowiednie współrzędne $x_p,y_p$. Ostatecznie, obraz jest reprezentowany przez prostokątną matrycę $m×n$ pikseli, gdzie m i n reprezentują liczby pikseli, odpowiednio w poziomie i w pionie. Liczby te określają tak zwaną rozdzielczość pikselową obrazu, na przykład 1920 x 1080. Tak określona rozdzielczość obrazu jest niezależna od rzeczywistych rozmiarów obrazu - precyzuje jedynie za pomocą ilu pikseli obraz jest reprezentowany. W praktyce spotyka się różne rozdzielczości pikselowe. Obecnie najczęściej spotyka się rozdzielczości pikselowe dla których stosunek wartości rozdzielczości poziomej do wartości rozdzielczości pionowej wynosi 16/9. Dawniej stosunek ten wynosił najczęściej 4/3.

Obok rozdzielczości pikselowej obrazu spotyka się również tak zwaną rozdzielczość liniową obrazu (ppi), która określa liczbę pikseli wyświetlanych na odcinku 1 cala. Wartość ta jest istotna przy określaniu wielkości obrazu reprodukowanego na różnych urządzeniach. W odniesieniu do drukarek korzysta się z podobnego parametru (dpi) określającego liczbę punktów, które może drukarka wydrukować na odcinku 1 cala.

Obraz przedstawiony w postaci matrycy pikseli jest określany często jako mapa pikseli; w praktyce stosowane są również określenia: mapa bitowa oraz bitmapa, niezależnie od tego ile bitów jest wykorzystywanych do reprezentacji piksela.

Dla zapamiętania obrazu w postaci mapy pikseli potrzebna jest odpowiednia ilość miejsca w pamięci. Dla przykładu, jeżeli obraz ma rozdzielczość pikselową 1920 x 1080 i barwa pojedynczego piksela jest reprezentowana za pomocą 24 bitów, to do zapamiętania informacji o obrazie potrzeba (1920 x 1080 x 24) bitów w pamięci (około 49,77 Mb lub 6,22 MB).

Rozdzielczość pikselowa obrazu nie jest cechą stałą obrazu. Obraz może być przedstawiony z różnymi rozdzielczościami, zależnie od potrzeb bądź od możliwości urządzeń próbkujących, pamiętających czy wyświetlających. Oczywiście, im większa rozdzielczość obrazu tym lepsza aproksymacja rzeczywistego obrazu. Na rysunku II.3 jest pokazany ten sam obraz przy dwóch różnych rozdzielczościach pikselowych.

Rys. II.3. Obraz przedstawiony z różnymi rozdzielczościami pikselowymi

Podobnie jak w przypadku rozdzielczości pikselowej obrazu, również liczba bitów poświęcanych na reprezentację barwy pojedynczego piksela nie jest cechą charakterystyczną obrazu. Przy większej liczbie bitów uzyskujemy wierniejsze odzwierciedlenie rzeczywistej barwy. Na rysunku II.4 pokazano ten sam obraz wyświetlony przy dwóch różnych liczbach bitów reprezentujących barwę pojedynczego piksela; w obu przypadkach rozdzielczość pikselowa obrazu jest taka sama.

Rys. II.4. Obraz przy różnych liczbach bitów na piksel

Jednak nadmierne zwiększanie liczby bitów reprezentujących barwę piksela napotyka barierę sensowności, wynikającą z ograniczonych możliwości postrzegania barw przez człowieka. Na ogół uważa się, że dla potrzeb fotorealistycznych obrazów wystarcza 8 bitów dla zakodowania informacji o luminancji albo o każdej z podstawowych barw R,G,B. Czasami może występować potrzeba zwiększenia tej wartości do 10 lub 12 bitów.

W praktyce komputerowej są stosowane ekrany o różnych rozdzielczościach pikselowych. W miarę upływu czasu i rozwoju technologii rozdzielczości te rosną - kiedyś było to 320 x 240 obecnie „typowa” wartość to 1920 x 1080. Można postawić pytanie czy są jakieś granice dla zwiększania rozdzielczości monitorów. Wydaje się, że jedyne sensowne ograniczenie można wiązać ze skończoną zdolnością systemu wzrokowego człowieka do rozróżniania szczegółów. Praktyczna reguła mówi, że człowiek jest w stanie rozróżniać szczegóły widziane w obrębie kąta o wartości około 1 minuty kątowej. Przyjmując, że typowa odległość obserwatora od ekranu monitora wynosi około 0,5 metra można określić sensowną rozdzielczość odnośnie do postrzegania drobnych szczegółów.

Przykład

Obserwator ogląda obraz o szerokości 30 cm z odległości 50 cm. Przyjmując, że obserwator jest w stanie rozróżniać szczegóły widziane w obrębie kąta o wartości 1 minuty kątowej (1’) określić przybliżoną liczbę pikseli w poziomie, które obserwator jest w stanie rozróżnić.

Korzystając z rysunku pokazanego obok możemy zapisać, że $tg α/2=0,3$. Stąd $α/2≅17°$ i $α≅34°$. Przy założonej zdolności rozróżniania szczegółów i pamiętając, że $1°=60’$ otrzymujemy szukany wynik

$34∗60=2040$ pikseli

Czasami powstaje konieczność zmiany rozdzielczości obrazu. W ogólnym przypadku obliczenia związane ze zmianą rozdzielczości można zrealizować w następujący sposób. Załóżmy, że mamy sytuację jak na rysunku II.5a. Na siatkę prostokątną istniejącego obrazu nałożona jest nowa siatka prostokątna (zaznaczona pogrubionymi liniami) o docelowej rozdzielczości. Znane są wartości skoków obu siatek. Na rysunku II.5b jest pokazany w powiększeniu fragment oznaczony kółkiem na rysunku II.5a.

Rys. II.5. Zmiana rozdzielczości przy punktowej reprezentacji pikseli

Problem polega na znalezieniu wartości piksela N z nowej siatki jeżeli znane są wartości (jasności) pikseli A, B, C, D w obrazie o początkowej rozdzielczości. Zakładamy, że znane są wartości α i β określające położenie piksela N w kwadracie ABCD.

Weźmy pod uwagę piksele A i B. Metodą interpolacji możemy znaleźć wartość jasności w pomocniczym punkcie P1, leżącym na odcinku AB i dzielącym ten odcinek w stosunku α : (1-α), jako

P1 = α B + (1 - α) A.

Analogicznie możemy znaleźć wartość jasności dla punktu P2 leżącego między pikselami C i D , jako

P2 = α D + (1 - α) C.

Wreszcie, znając wartości jasności w punktach P1 i P2, korzystając jeszcze raz z metody interpolacji, możemy znaleźć wartość jasności dla piksela N, jako

N = β P2 + (1 - β) P1.