Modelowanie obiektów i scen 3D

Modelowanie obiektów

Wśród różnych metod modelowania obiektów trójwymiarowych można wyróżnić dwie grupy metod: metody bazujące na opisie powierzchni bocznej bryły (metody Brep) oraz metody objętościowe.

W grupie metod Brep wykorzystuje się zarówno metody opisujące dokładnie powierzchnię modelowanej bryły (tzw. metody powierzchniowe), jak też metody przybliżające powierzchnię bryły, zwłaszcza metody przybliżające powierzchnię zewnętrzną bryły za pomocą siatki wielokątów, najczęściej trójkątów.

Metody objętościowe, to przede wszystkim metody wokselowe.

Siatki wielokątowe

W większości zastosowań do opisania powierzchni zewnętrznej wykorzystuje się siatki wielokątowe - powierzchnia boczna bryły jest opisywana za pomocą zbioru wielokątów. W przypadku takich brył jak wielościany reprezentacja ta jest w pełni naturalna. W przypadku gdy powierzchnie boczne nie są płaskie dokonuje się aproksymacji wielokątowej tych powierzchni.

Na rysunku VI.1 pokazano przykłady aproksymacji powierzchni bocznych kilku obiektów za pomocą wielokątów. Między innymi pokazano dwie reprezentacje powierzchni kuli - proszę się zastanowić nad sposobami uzyskania takich reprezentacji kuli oraz nad różnicami między tymi reprezentacjami.

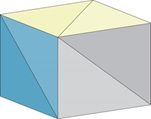
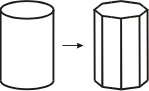
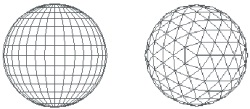
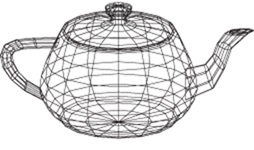
Rys. VI.1. Przykłady wielokątowej aproksymacji powierzchni obiektów

Zwróćmy uwagę na sposób opisywania takich siatek. Z reguły korzysta się z dwóch tabel. Jedna z nich służy do przechowywania informacji o wierzchołkach siatki a druga do przechowywania informacji o poszczególnych wielokątach. Przykład opisu tego typu jest pokazany na rysunku VI.2.

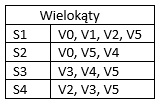
Rys. VI.2. Sposób opisywania siatek wielokątów

Zaletą takiego opisu jest oszczędność miejsca w pamięci (każdy wierzchołek jest zapisany tylko raz) oraz to, że przy ewentualnych przekształceniach geometrycznych obliczenia związane z danym wierzchołkiem są wykonywane tylko raz (proszę się zastanowić co by było gdyby każdy wielokąt był opisywany niezależnie).

W praktyce często wykorzystuje się siatki trójkątów. Wynika to z faktu, że każdy trójkąt jednoznacznie wyznacza powierzchnię na której leży. Liczba wielokątów (trójkątów) aproksymujących złożony obiekt może być bardzo duża. Niczym wyjątkowym są przypadki aproksymowania powierzchni za pomocą kilkuset tysięcy trójkątów. Im więcej szczegółów zawiera powierzchnia boczna obiektu, tym więcej trójkątów potrzeba do jej aproksymacji. Należy jednak pamiętać o konieczności zachowania kompromisu między dokładnością modelowania powierzchni a czasem potrzebnym do jej renderowania - im więcej wielokątów tym dłuższy czas renderingu.

Poprawna siatka trójkątów powinna być ciągła (pozbawiona dziur). Siatka taka powinna cechować się tym, że każda krawędź siatki powinna należeć tylko do dwóch trójkątów (ewentualnie do jednego trójkąta, jeżeli jest to trójkąt brzegowy siatki) oraz tym, że każdy wierzchołek siatki ma jeden ciągły zestaw trójkątów wokół siebie. Ponadto siatka powinna być poprawnie zorientowana. Oznacza to, że wszystkie wektory normalne do poszczególnych trójkątów powinny być skierowane na zewnątrz bryły.

Generowanie siatek w przypadku prostych brył na ogół nie nastręcza trudności. Natomiast w przypadku brył o złożonych powierzchniach bocznych, często jedynym sensownym rozwiązaniem jest wykonanie rzeczywistego modelu bryły a potem wykorzystanie ręcznego skanera do pozyskiwania współrzędnych punktów leżących na powierzchni bryły - punkty te będą stanowiły wierzchołki tworzonej siatki.

Istniejąca siatka trójkątów może być, zależnie od potrzeb, zagęszczana (poprzez podział trójkątów siatki na mniejsze trójkąty) jeżeli potrzebna jest większa dokładność modelu albo upraszczana (poprzez usuwanie krawędzi albo wierzchołków siatki) w przeciwnym przypadku. Upraszczanie siatek jest wykorzystywane na przykład wtedy gdy obiekt modelowany oddala się - wtedy dokładność prezentacji jego wyglądu przestaje mieć znaczenie. W tym kontekście, w grafice występuje pojęcie poziomu dokładności (z ang. LOD - Level of Detail).

Modele powierzchniowe

Modele powierzchniowe zapewniają dokładny opis powierzchni bocznej obiektu. Wyróżnia się powierzchnie uwikłane i powierzchnie parametryczne.

Powierzchnie uwikłane opisywane są równaniami o postaci

$$f(x,y,z)=0$$

W tym przypadku istnieje bezpośrednia zależność między powierzchnią a punktem w przestrzeni - punkt może leżeć na powierzchni, wewnątrz powierzchni albo na zewnątrz powierzchni. Nie wnikając w szczegóły, zasygnalizujmy tylko, że są kategorie powierzchni algebraicznych (wielomianowych) i niealgebraicznych (na przykład powierzchnie reprezentowane za pomocą zbioru cząstek).

W przypadku powierzchni parametrycznych położenie punktu na powierzchni P(u,v) opisuje się za pomocą dwóch parametrów bieżących. Powierzchnie są definiowane za pomocą punktów sterujących. Przykładowymi powierzchniami tego typu są powierzchnie Béziera opisywane za pomocą zależności

$$P(u,v)=∑↙{j=0}↖m∑↙{k=0}↖n P_{j,k}B_{j,m}(v)B_{k,n}(u)$$

gdzie $P_{j,k}$ są punktami sterującymi a $B_{j,m}(v)$ oraz $B_{k,n}(u)$ odpowiednimi funkcjami bazowymi. Powierzchnię Béziera opisują dwa zbiory krzywych Béziera prowadzonych w płaszczyznach prostopadłych do siebie. Poglądowo ilustruje to rysunek VI.3.

Rys. VI.3. a) Przykładowa powierzchnia Béziera, b) Powierzchnia obiektu wyznaczona za pomocą płatów Béziera

Zaletą powierzchni Béziera jest to, że manipulując położeniami punktów sterujących można łatwo modyfikować kształt powierzchni. Często model powierzchni składa się z kilku części (tzw. płatów Béziera).

Modele wokselowe

Idea modelowania wokselowego polega na tym, że modelowany obiekt jest umieszczany we wnętrzu sześcianu. Z kolei sześcian jest dzielony kolejno na coraz mniejsze podsześciany aż do poziomu najmniejszego wymaganego podsześcianu. Ten najmniejszy podsześcian jest określany jako woksel. Następnie sprawdza się, które woksele należą do modelowanego obiektu. Zbiór tych wokseli jest szukanym modelem obiektu.

Metoda wokselowa jest bardzo wymagająca jeśli chodzi o pojemność pamięci potrzebnej do zapamiętania informacji o obiekcie. Załóżmy dla przykładu, że ograniczamy precyzję modelu do sześcianu o boku 512 jednostek. Oznacza to, że musimy liczyć się z koniecznością zarezerwowania miejsca w pamięci dla przechowania informacji o 512³ wokselach (a nie jest to wcale duża rozdzielczość w stosunku do potrzeb).

Z kolei zaletą metody jest to, że z każdym wokselem można związać dodatkową informację w postaci odpowiednich atrybutów. Uzyskujemy w ten sposób model, który dostarcza informację nie tylko o tym, które woksele należą do obiektu 3D, ale również o innych cechach poszczególnych elementów wnętrza obiektu. Tworząc na przykład model wokselowy jakiejś części ciała człowieka można z każdym wokselem związać informację o tym czy w danym miejscu jest tkanka miękka, tkanka kostna, naczynie krwionośne itd. Mając taki model, można z kolei wyznaczać różne przekroje ciała człowieka i na przykład poznawać anatomię człowieka.

O ile metoda wokselowa niesie informacje o wnętrzu obiektu, to bezpośrednio nie jest dostępna informacja o powierzchni zewnętrznej obiektu.

Metody wspomagające modelowanie

W programach grafiki 3D są wykorzystywane różne metody ułatwiające proces modelowania. Omówimy tu dwie spośród takich metod: metodę CSG oraz metodę zakreślania.

W metodzie CSG (ang. Constructive Solid Geometry) zakłada się, że dostępny jest zestaw podstawowych brył (tak zwanych prymitywów), z których można tworzyć bryły bardziej złożone. Wykorzystuje się przy tym operacje boolowskie: łączenie brył ze sobą, znajdowanie części wspólnej brył oraz odejmowanie brył od siebie. Na rysunku VI.4 pokazano przykłady ilustrujące działanie tych operacji.

Rys. VI.4. Przykłady operacji wykonywanych w metodzie CSG. a) Dodawanie brył, b) odejmowanie brył, c) część wspólna brył

Kolejna metoda modelowania brył określana jest jako metoda przesuwania przekroju (ang. sweeping) albo zakreślania. W metodzie tej definiowany jest przekrój bryły, który następnie jest przesuwany wzdłuż zadanej ścieżki. W czasie przesuwania jest wyznaczana powierzchnia boczna bryły. Ścieżka może być linią prostą albo krzywą (na przykład krzywą Béziera). W czasie przesuwania przekrój bryły może się zmieniać. W szczególnym przypadku, gdy przekrój jest obracany wokół pewnej osi możliwe jest tworzenie brył obrotowych. Na rysunku VI.5 pokazano przykład ilustrujący działanie metody.

Rys.VI.5. Modelowanie metodą przesuwania przekroju

Programy grafiki 3D udostępniają również narzędzia umożliwiające modyfikowanie, czy też deformowanie przygotowanych wcześniej modeli. Obiekty mogą być na przykład skręcane, wyginane, przewężane, rozciągane itd. Przykłady takich modyfikacji pokazano na rysunku VI.6.

Rys. VI.6. Przykłady modyfikacji obiektów 3D

Atrybuty modeli

Etap modelowania obiektów dostarcza informacji o kształcie obiektu. Konieczne jest jeszcze określenie atrybutów obiektu, które umożliwią późniejszy poprawny rendering. W szczególności, trzeba określić parametry powierzchni obiektu (kolor, materiał), parametry istotne dla teksturowania itp. Rodzaj materiału decyduje o właściwościach refleksyjnych powierzchni (czasami również o właściwościach emisyjnych powierzchni). Pozwala to modelować obiekty o powierzchniach pochłaniających, matowych, lśniących, błyszczących czy odbijających zwierciadlanie. Dodajmy od razu, że końcowy widok obiektu będzie dodatkowo zależał od jego oświetlenia, kąta obserwacji itd. Atrybuty modeli często są przypisywane wierzchołkom siatek trójkątnych przybliżających powierzchnie boczne.

Źródła światła

Niezbędnym elementem scen 3D są źródła światła, dzięki którym możliwe jest „oglądanie” obiektów znajdujących się w scenie a także wyznaczanie barw powierzchni bocznych tych obiektów.

W rzeczywistości źródła światła są obiektami, które mają kształt i wymiary tak jak inne obiekty, ale dodatkowo emitują światło. W grafice komputerowej źródła światła najczęściej są traktowane jako obiekty idealizowane bez wymiarów - wyróżnia się światła punktowe i kierunkowe (odległe). Wykorzystuje się również światła powierzchniowe.

Światło punktowe jest umieszczane w określonym punkcie sceny. Światło takie generuje promienie rozchodzące się we wszystkich kierunkach jednakowo. Promienie docierają do określonego obiektu pod różnymi kątami (por rys. VI.7a).

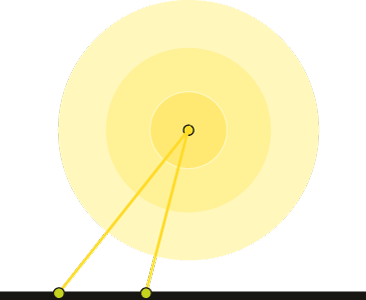
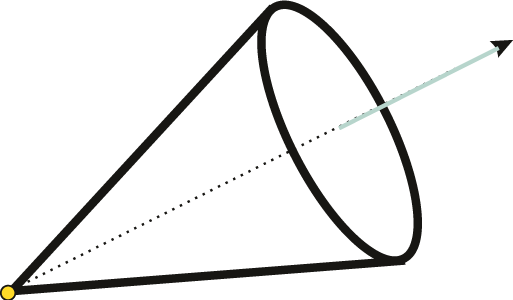
Rys. VI.7. Źródło światła: a) punktowe, b) stożkowe

Ze źródłem światła mogą być związane różne parametry, takie jak współrzędne położenia (x,y,z), barwa, intensywność, funkcja tłumienia w zależności od odległości d (na przykład $f=1/{d^2}\;$). Światła punktowe nie podlegają obrotom i skalowaniu, natomiast mogą być przesuwane w scenie.

Czasami można ograniczać zakres rozchodzenia się światła punktowego, na przykład do wnętrza stożka o określonym kącie rozwarcia i kierunku osi głównej stożka (por. rys.VI.7b).

Światła kierunkowe symulują światła znajdujące się w tak dużej odległości, że można przyjąć, że promienie światła docierające do obiektu są do siebie równoległe (rys. VI.8). W takiej sytuacji istotny jest kierunek z którego docierają promienie, natomiast położenie źródła światła nie ma znaczenia i nie podlega operacji translacji.

Rys. VI.8. Światło kierunkowe

W przypadku rzeczywistych świateł powierzchniowych cała powierzchnia światła emituje światło we wszystkich kierunkach. W grafice komputerowej światła powierzchniowe są realizowane w ten sposób, że na określonej powierzchni rozmieszcza się pewną liczbę świateł punktowych. Korzystanie ze świateł powierzchniowych jest istotne wtedy gdy istnieje potrzeba generowania miękkich cieni rzucanych przez obiekty.

Modelowanie sceny

Po opracowaniu modeli poszczególnych obiektów i określeniu ich atrybutów można przystąpić do projektowania sceny, która będzie potem renderowana i prezentowana na ekranie. Projektowanie sceny polega na przeniesieniu przygotowanych modeli obiektów składowych do jednego układu współrzędnych (tak zwanego układu świata) i umieszczeniu ich w odpowiednich pozycjach. Wykorzystuje się przy tym operacje zmiany układów współrzędnych oraz przekształcenia geometryczne.

Dla pełnego zdefiniowania sceny konieczne jest jeszcze określenie tła i określenie sposobu oświetlenia sceny, a więc dobranie i rozmieszczenie w scenie źródeł światła punktowych, kierunkowych, stożkowych. Często definiuje się również tzw. światło otoczenia. Światło to nie jest związane z żadnym konkretnym źródłem światła. Natomiast pozwala ono uwzględniać fakt, iż w rzeczywistości obiekty są widoczne nawet wtedy gdy do powierzchni obiektu nie dociera bezpośrednio światło z dostępnych źródeł światła.

Na rysunku VI.9 pokazano przykładową bryłę oświetloną przez różne źródła światła.

Rys. VI.9. Bryła oświetlona przez różne źródła światła

Zdefiniowana scena może być oglądana z różnych punktów obserwacji i pod różnymi kątami. W celu określenia sposobu obserwacji sceny wprowadza się pojęcie kamery (obserwatora). Parametry kamery określają jej położenie, orientację i kierunek patrzenia. Parametry te umożliwiają określenie położenia umownego ekranu na którym będzie prezentowany dwuwymiarowy widok sceny 3D.

Cienie rzucane przez obiekty

W rzeczywistym świecie, przy odpowiednim oświetleniu, z poszczególnymi obiektami zawsze związane są cienie rzucane przez te obiekty. W grafice 3D problem ten również musi być uwzględniony. Zależnie od rodzaju oświetlenia obiekt może rzucać cień pełny albo cień pełny oraz półcień.

Jeżeli obiekt jest oświetlony przez punktowe źródło światła, to na podłożu jest generowany obszar cienia pełnego (rys. VI.10). W celu wyznaczenia obszaru cienia na podłożu trzeba ze źródła światła poprowadzić promienie styczne do obiektu i znaleźć ich przecięcia z podłożem. Następnie trzeba odtworzyć obszar cienia i nadać mu odpowiednią barwę.

Rys. VI.10. Obszar cienia pełnego

Żeby uzyskać obszary cienia pełnego oraz półcienia konieczne jest użycie źródła światła powierzchniowego (rys. VI.11). Jeżeli światło powierzchniowe jest modelowane jako zbiór świateł punktowych rozmieszczonych na powierzchni, to trzeba rozpatrzeć każde źródło punktowe niezależnie. Obszar cienia pełnego będzie określony jako ten do którego nie dociera żaden promień. Obszar półcienia będzie określony jako ten do którego docierają poszczególne promienie. Odcień szarości poszczególnych punktów w obszarze półcienia będzie określony w zależności od liczby promieni docierających do danego punktu.

Rys. VI.11 Obszary cienia pełnego i półcienia

W obliczeniach związanych z cieniami w scenie wykorzystuje się metody przyspieszające obliczenia. W jednej z nich wykorzystuje się tzw. bryłę cienia. Dla określonego źródła światła punktowego i pewnego obiektu można wyznaczyć fragment przestrzeni do której nie będzie docierał żaden promień ze źródła światła. Ten fragment przestrzeni jest określany jako bryła cienia. Na rysunku VI.12 pokazana jest bryła cienia dla kombinacji: punktowe źródło światła i trójkąt. Znajomość bryły cienia umożliwia szybkie sprawdzanie czy jakiś obiekt, lub jego część, leży w cieniu czy nie.

Rys. VI.12. Bryła cienia

Inna koncepcja jest wykorzystana w metodzie mapy cienia. W fazie preprocesingu, poprzedzającego obliczenia związane z obserwacją sceny z różnych położeń kamery, wykonuje się obliczenia, które później ułatwią ocenianie czy określony punkt leży w cieniu czy nie.

W tym celu między punktowym źródłem światła a sceną umieszcza się pomocniczy ekran, określany tu jako mapa cieni. Dla każdego piksela tej mapy prowadzi się ze źródła światła promień w stronę sceny i po znalezieniu pierwszego trafionego obiektu określa się odległość między trafionym punktem a źródłem światła. Odległość ta jest zapisywana jako atrybut piksela mapy cienia.

Po umieszczeniu w scenie kamery, z której będzie oglądana scena, prowadzi się promień z kamery przez piksel ekranu w stronę sceny. Po znalezieniu pierwszego trafionego obiektu oblicza się odległość punktu przecięcia P promienia z obiektem a źródłem światła. Jeżeli znaleziona odległość jest równa wartości zapisanej w mapie cienia to punkt P nie leży w cieniu. W przeciwnym przypadku punkt P leży w cieniu.

Przekształcenia geometryczne obiektów 3D

Uzyskane modele brył mogą być poddawane różnym przekształceniom geometrycznym: przesuwaniu, obrotom, skalowaniu itd. Wykorzystuje się przy tym najczęściej koncepcję współrzędnych jednorodnych, podobnie jak w grafice 2D na płaszczyźnie. Z tym, że teraz każdy punkt jest reprezentowany za pomocą czterech współrzędnych (x,y,z,1). Macierze dla podstawowych przekształceń są pokazane niżej.

Przesunięcie o wektor ($t_x$, $t_y$, $t_z$)

Skalowanie ze współczynnikami skalowania $S_x$, $S_y$, $S_z$

W przypadku obrotów są trzy macierze, odpowiednio dla obrotu wokół osi x, wokół osi y i wokół osi z. W prawoskrętnym układzie współrzędnych dodatni kąt obrotu oznacza obrót w kierunku przeciwnym do ruchu wskazówek zegara jeżeli patrzy się wzdłuż osi w kierunku początku układu współrzędnych.

Obrót wokół osi x

Obrót wokół osi y

Obrót wokół osi z

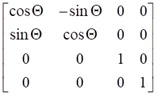
Możliwe jest również składanie przekształceń i wyznaczanie macierzy wypadkowej dla określonego ciągu przekształceń. W szczególności, można w ten sposób znaleźć macierz obrotu wokół innej osi niż jedna z osi układu współrzędnych.

Bardziej złożone obiekty mogą być modelowane z wykorzystaniem koncepcji hierarchii. Elementy składowe obiektu mogą być łączone w jedną wspólną strukturę. Wtedy zastosowanie transformacji do jednego obiektu przenosi się na obiekty z nim związane.

Układy współrzędnych

W fazie modelowania poszczególne obiekty mogą być tworzone w swoich układach współrzędnych. Przy tworzeniu bardziej złożonego obiektu, konieczne jest przeniesienie obiektów składowych do jednego wspólnego układu współrzędnych. Na przykład, przy modelowaniu samochodu nadwozie, podwozie i koła mogą być modelowane w zupełnie niezależnych układach. Jednak przy tworzeniu modelu całego samochodu poszczególne elementy muszą być połączone w jednym wspólnym układzie współrzędnych. Z kolei cały model samochodu może być przeniesiony do układu współrzędnych sceny. Najwyższy poziom układów współrzędnych jest określany jako układ współrzędnych świata.

Zmiana układu współrzędnych polega na wykonaniu ciągu przekształceń geometrycznych: obrotów, przesunięć i skalowania. Problem ten ilustruje rysunek VI.13. W układzie współrzędnych A(x,y,z) znajduje się inny układ współrzędnych B(x’,y’.z’), którego początek znajduje się w punkcie (x₀,y₀,z₀) i którego osie są skierowane zgodnie z wersorami u_x',u_y',u_z'. Przejście z tego układu współrzędnych B do układu A wymaga wykonania operacji przesunięcia początku układu współrzędnych B o wektor T(-x₀,-y₀,-z₀) a następnie wykonania obrotu, który zapewni pokrycie się osi obu układów. Obrót ten można wykonać korzystając z macierzy R, w której zapisane są wektory składowe wersorów osi układu B. Ewentualnie, konieczne może być również wykonanie skalowania osi układu B, tak żeby uzyskać zgodność wymiarowania osi w obu układach.

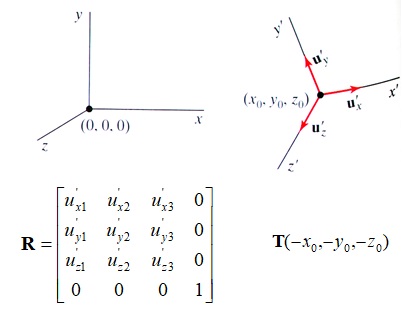
Rys. VI.13. Zmiana układu współrzędnych