Animacja

Tworzenie filmów animowanych ma długą historię. W naturalny sposób, pojawienie się komputerów spowodowało dalszy szybki rozwój animacji. W wykładzie zostaną przedstawione wybrane zagadnienia charakteryzujące sposoby wykorzystywania komputerów w animacji.

Dotychczas zajmowaliśmy się tworzeniem pojedynczego - statycznego obrazu. Jednak otaczająca nas rzeczywistość nie jest statyczna i metody grafiki komputerowej muszą umożliwić również rozwiązanie problemu wizualizacji zmian zachodzących w funkcji czasu. Zajmuje się tym animacja komputerowa. W animacji generowane są zestawy klatek (obrazów, ramek) odzwierciedlających wygląd sceny w kolejnych, dyskretnych chwilach. Z kolei, dzięki pewnej bezwładność naszego systemu wzrokowego, przy dostatecznie szybkim wyświetlaniu kolejnych klatek uzyskuje się wrażenie ciągłości zmian zachodzących w funkcji czasu.

Warto tu od razu zaznaczyć, że animacja nie ogranicza się jedynie do ruchu - każda zmiana występująca między kolejnymi klatkami jest pewną formą animacji. Tak więc na przykład, zmiana kształtu obiektu czy zmiana wyglądu obiektu, to też są pewne formy animacji. Zauważmy również, że przy wyświetlaniu sekwencji obrazów, kolejne obrazy można traktować jako próbki ciągłej sekwencji rzeczywistych zdarzeń, pobierane w określonych odstępach czasu. Sekwencja klatek tworzących animację jest tworzona off-line i można ją wyświetlać z wymaganą częstotliwością.

Koncepcja animacji komputerowej jest podobna do klasycznej animacji, kiedy to główny animator rysował ręcznie ramki kluczowe dla animowanej sekwencji, a asystenci rysowali na tej podstawie ramki pośrednie. W animacji komputerowej główny animator przy rysowaniu ramek kluczowych wykorzystuje odpowiednie programy grafiki komputerowej. Klatki pośrednie są wyznaczane komputerowo.

Przy tworzeniu animacji dla parametru, którego wartości zmieniają się w funkcji czasu trzeba wyróżnić klatki kluczowe. Dla każdej z tych klatek animator musi określić wartość parametru. Wartości dla klatek pośrednich oblicza komputer zgodnie z wybranym sposobem interpolacji, liniowej bądź nieliniowej, wartości z klatek kluczowych.

Często, w funkcji czasu, zmieniają się wartości wielu parametrów, niekoniecznie w tych samych chwilach. Wtedy wygodnie jest zapisywać informacje o chwilach zmian tych parametrów w postaci zbiorczego diagramu, na przykład takiego jak na rysunku IX.1. Na rysunku uwzględniono 6 parametrów. Dla każdego z nich, odpowiednim kolorowym punktem, zaznaczono klatki kluczowe.

Rys. IX.1. Poglądowy zapis informacji o chwilach, w których mają następować zmiany wartości poszczególnych parametrów. Punkty o określonym kolorze wyróżniają klatki kluczowe danego parametru

Na rysunku IX.2 pokazano przykład wyznaczania trzeciej klatki pośredniej dla trójkąta zmieniającego położenie między klatkami kluczowymi pierwszą i piątą, przy założeniu, że wykorzystywana jest interpolacja liniowa. Zwróćmy uwagę, że interpolację wykonuje się w odniesieniu do wierzchołków trójkątów. Oznacza to, że wcześniej zostały określone położenia poszczególnych wierzchołków w klatkach kluczowych.

Rys. IX.2. Przykład wyznaczania klatki pośredniej

Najpierw łączy się odcinkami odpowiadające sobie punkty (wierzchołki) obu trójkątów. Następnie wyznacza się metodą interpolacji liniowej położenia punktów dla klatek pośrednich. Dla uproszczenia, na rysunku IX.2 pokazano tylko jedną klatkę pośrednią K3, leżącą w połowie drogi między klatkami K1 i K5.

W ogólnym przypadku, przy przemieszczaniu się dowolnego obiektu w funkcji czasu, trzeba liczyć się z koniecznością wykonywania interpolacji położenia obiektu, interpolacji obrotu obiektu, sterowania szybkością przemieszczania się obiektu, interpolacją innych parametrów obiektu.

Na początku zawsze istotne jest określenie toru wzdłuż którego następuje zmiana parametru. Tor ten musi być określony na podstawie znajomości wartości parametru P w kolejnych klatkach kluczowych (rys. IX.3). Po wyznaczeniu toru można obliczyć wartości parametru P w klatkach pośrednich.

Rys. IX.3. Przykładowy tor poruszania się obiektu zdefiniowany przez wartości parametru P w klatkach kluczowych

W ogólnym przypadku tor ten może być krzywoliniowy. W przykładzie z rysunku IX.3 tor został określony za pomocą krzywej interpolującej punkty z klatek kluczowych. Wykorzystuje się tu na przykład krzywe Hermite’a. Są to krzywe trzeciego stopnia składające się z łuków Hermite’a. Każdy łuk Hermite’a łączy dwa sąsiednie punkty, dla których poza położeniem znane są wektory pochodnych w tych punktach. Możliwe jest również sterowanie prędkością i przyspieszeniem poruszania się obiektu po wybranym torze.

W czasie przesuwania się obiektu po torze, obiekt może równocześnie obracać się. W związku z tym powstaje problem interpolacji obrotu między dwoma kątami, początkowym i końcowym, określonymi w klatkach kluczowych. Okazuje się, że klasyczny sposób przeliczania obrotów za pomocą odpowiednich macierzy we współrzędnych jednorodnych czasami zawodzi. Efekt taki może wystąpić wtedy gdy w czasie obliczeń dojdzie do tego, że dwie z trzech osi układu współrzędnych znajdą się na jednej linii (pokryją się) co prowadzi do tzw. blokady przegubu (ang. gimbal lock). W związku z tym, do wykonywania interpolacji obrotów wykorzystuje się najczęściej rachunek kwaternionów. Bazuje się przy tym na twierdzeniu Eulera o obrotach, zgodnie z którym, do dowolnego położenia kątowego można przejść z innego położenia za pomocą jednego obrotu według pewnej osi (w szczególności osi przechodzącej przez początek układu współrzędnych). Korzystając z rachunku kwaternionów mamy gwarancję, że nie wystąpi efekt blokady przegubu.

Jednym z trudniejszych obiektów, z którymi można się spotkać przy tworzeniu animacji jest postać człowieka. Jeśli chodzi o model człowieka, to z reguły najpierw modeluje się szkielet, na który później „naciąga się” ciało i skórę Szkielet konstruowany jest z brył sztywnych połączonych złączami obrotowymi albo przegubami kulistymi. Sterowanie ruchami człowieka (szkieletu) jest trudnym zadaniem ze względu na dużą liczbę złącz i różnych ograniczeń. Dlatego też, w praktyce wykorzystuje się koncepcję przechwytywania ruchu (motion capture). Polega ona na tym, że jeżeli na przykład w animacji jakaś osoba ma wykonać pewną sekwencję ruchów, to można wynająć aktora i w różnych miejscach ciała można rozmieścić zestaw odpowiednich markerów albo czujników. Następnie, w czasie gdy aktor będzie wykonywał zakładaną sekwencję ruchów, rejestruje się kolejne położenia markerów albo czujników w funkcji czasu. Na podstawie tak uzyskanych informacji można wiernie odtworzyć ruch animowanej osoby. Na podobnej zasadzie można też rozwiązać problem animacji mimiki twarzy.

Obiekt poruszający się w scenie może wchodzić w kolizje z innymi obiektami. W poprawnie wykonanej animacji powinno się wykrywać fakt wystąpienia kolizji oraz odpowiednio reagować na ten fakt. Sposób ustalania chwili, w której następuje kolizja nie jest oczywisty. Wynika to stąd, że między dwoma klatkami animacji upływa pewien czas. Jeżeli w jednej klatce jeszcze nie będzie kolizji, to w następnej może już być po kolizji i jeden obiekt już zaczął wnikać w drugi obiekt. Dopuszczenie do sytuacji wnikania jednego obiektu w drugi nie jest najlepszym rozwiązaniem. Stąd, najlepiej jest przyjmować, że kolizja występuje wcześniej niż faktycznie do niej dojdzie. Znając odległość obiektów i ich prędkości, można oszacować kiedy dojdzie do kolizji i za moment wystąpienia kolizji przyjąć klatkę poprzedzającą ten fakt.

Przy wyznaczaniu kolizji istotny jest sposób stwierdzania czy doszło do kolizji. Wyjaśnijmy to na przykładzie dwóch poruszających się sześcianów. Na pierwszy rzut oka może się wydawać, że wystarczy sprawdzać czy któryś z wierzchołków jednego sześcianu nie znajduje się już we wnętrzu drugiego sześcianu, tak jak na rysunku IX.4a. Trzeba jednak uwzględnić możliwość wystąpienia takiej sytuacji jak na rysunku IX.4b - żaden z wierzchołków jednego sześcianu nie znajduje się we wnętrzu drugiego sześcianu a do kolizji już doszło.

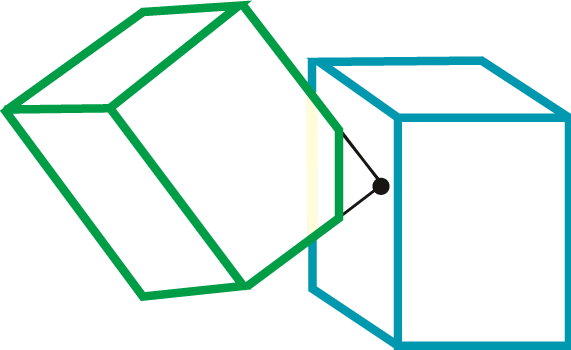
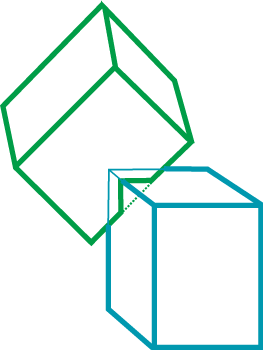
Rys. IX.4. Ilustracja problemu sprawdzania kolizji

Po wykryciu kolizji istotne jest określenie zachowania się kolidujących obiektów. Sposób reakcji zależy od wielu czynników. Ale w większości przypadków konieczne jest przestrzeganie praw fizyki. Przykładowo, jeżeli piłka rzucona do góry po pewnym czasie spada na ziemię, to trzeba określić nowy kierunek ruch piłki i jej prędkość początkową tak, żeby nie mogła polecieć wyżej niż poprzednio.

Jedną z technik animacji jest deformowanie (modyfikowanie) obiektów, polegające na zmianie ich kształtów (używa się tu określenia warping). W najprostszym przypadku, można tu wykorzystać odpowiednie transformacje w odniesieniu do wierzchołków figur czy brył, albo w odniesieniu do punktów sterujących krzywych (na przykład krzywych Béziera) czy powierzchni krzywoliniowych.

Prosty sposób modyfikowania kształtu obiektu polega na przesunięciu jednego wierzchołka obiektu i propagowaniu przesunięcia do sąsiednich wierzchołków z uwzględnieniem stopniowego zmniejszania przesunięcia wierzchołków. Przykład takiego postępowania pokazano na rysunku IX.5.

Rys. IX.5. Przykład modyfikowania kształtu obiektu

W powyższym przykładzie mieliśmy do czynienia cały czas z tym samym obiektem - zmieniał się tylko jego kształt. W innym rodzaju animacji możemy spotkać się z przejściem od jednego obiektu do innego obiektu. Mówimy wtedy o operacji morfingu albo o metamorfozie. Na rysunku IX.6 pokazano prosty przykład morfingu, w którym ma miejsce stopniowe przejście od figury niebieskiej do figury żółtej wzdłuż zadanej krzywej.

Rys. IX.6. Przykład morfingu między obiektami pokazanymi na rysunku a) wzdłuż zadanej krzywej b)