Cieniowanie i teksturowanie

Cieniowanie płaskie

W najprostszym przypadku można ograniczyć się do cieniowania płaskiego, polegającego na tym, że każdy wielokąt aproksymujący powierzchnię boczną obiektu jest pokrywany jednolitą barwą. Wyjaśnijmy ten sposób cieniowania na przykładzie sześcianu, w oryginale niebieskiego, oświetlonego kierunkowym źródłem światła o intensywności $I_p$. W takim przypadku jasność poszczególnych ścianek sześcianu zależy od kąta padania promieni ze źródła światłą na daną ściankę.

Jasność ścianki wyznacza się w sposób zilustrowany na rysunku VIII.1 - jasność ścianki jest równa iloczynowi jasności źródła światła i cosinusa kąta między wektorem N normalnym do płaszczyzny ścianki a wektorem L skierowanym do źródła światła.

Rys. VIII.1. Zależność jasności ścianki od kąta padania promieni z kierunkowego źródła światła

Proces cieniowani sześcianu trzeba zacząć od określenia ścianek do których bezpośrednio docierają promienie ze źródła światła. Dla tych ścianek można określić kąty padania tych promieni na poszczególne ścianki i w konsekwencji odcień koloru niebieskiego.

Powstaje pytanie jaką barwę przypisać pozostałym ściankom, czyli tym do których nie docierają promienie ze źródła światła. Przypisanie tym ściankom barwy czarnej byłoby raczej niezgodne z naszą intuicją. Problem ten rozwiązuje się w ten sposób, że wprowadza się pojęcie światła rozproszonego - światła, które istnieje w całej scenie ale nie jest związane z żadnym źródłem światła. Uwzględniając istnienie światła rozproszenia można rozpatrywanym ściankom przypisać barwę ciemnoniebieską. Wartość światła otoczenia można również uwzględnić przy wyznaczaniu jasności ścianek widocznych ze źródła światła.

Po określeniu sposobu cieniowania ścianek sześcianu można określić położenie obserwatora w scenie, znaleźć ścianki widoczne z tego punktu i wyświetlić pocieniowany sześcian. Na rysunku VIII.2 pokazano widok sześcianu dla dwóch położeń obserwatora. Każda ścianka ma jednolity odcień barwy - stąd nazwa cieniowanie płaskie.

Rys. VIII.2. Sześcian oświetlony kierunkowym źródłem światła. a) Widok dla obserwatora znajdującego się w położeniu, z którego widać bezpośrednio trzy ścianki oświetlone przez źródło światła, przy czym promienie padają na ścianki 1, 2 i 3 pod różnymi kątami, b) widok dla obserwatora znajdującego się po przeciwnej stronie sześcianu niż źródło światła, w punkcie z którego widać trzy ścianki, które nie są bezpośrednio oświetlone przez źródło światła. Barwę ścianek 4, 5 i 6 określa przyjęte światło otoczenia

Cieniowanie gładkie

Model cieniowania płaskiego jest dobry w odniesieniu do prostych obiektów, których powierzchnie boczne składają się z niewielkiej liczby wielokątów. W przypadku gdy krzywoliniowe powierzchnie boczne obiektów są aproksymowane wielokątami (trójkątami) metoda cieniowania płaskiego nie daje dobrych rezultatów. Jeżeli każdy wielokąt jest pokryty jednolitą barwą, to może być widoczna struktura wielokątowa powierzchni aproksymującej (por. rysunek VIII.3). Efekt ten można usunąć wykorzystując cieniowanie gładkie, bazujące na metodzie Gouraud omówionej w wykładzie IV.

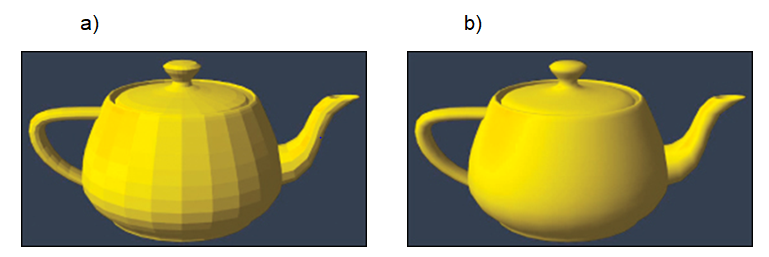
Rys. VIII.3. Przykłady cieniowania powierzchni kuli. a) Metoda cieniowania płaskiego, b) metoda cieniowania gładkiego

Załóżmy, że powierzchnia boczna bryły jest aproksymowana trójkątami i weźmy pod uwagę jeden trójkąt. Załóżmy ponadto, że znamy rzut tego trójkąta na płaszczyznę ekranu oraz, że znamy barwy (wartości jasności) trzech wierzchołków trójkąta (barwy te zostały wyznaczone w przestrzeni 3D przed rzutowaniem; sposób wyznaczania barw punktów powierzchni 3D jest omawiany dalej). W tej sytuacji możemy wyznaczyć barwy pikseli należących do trójkąta za pomocą metody Gouraud.

Zauważmy, że przy cieniowaniu dwóch trójkątów o wspólnej krawędzi uzyskuje się gładkie przejście cieniowania między obu trójkątami.

Równanie Phonga

Warunkiem koniecznym dla korzystania z cieniowania gładkiego jest znajomość barw wierzchołkowych poszczególnych trójkątów. Sposób wyznaczania tych barw można potraktować jako szczególny przypadek problemu wyznaczania barwy punktu powierzchni bocznej bryły w przestrzeni sceny.

Podstawowy sposób postępowania został zaproponowany przez Phonga i równanie przez niego zaproponowane znane jest jako równanie Phonga. Zostało ono określone przy następujących założeniach:

• Dostępne jest punktowe źródło światła
• Światło dociera do analizowanego punktu powierzchni z jednego kierunku i odbija się
• Uwzględnia się odbicie dyfuzyjne i odbicie zwierciadlane (w kierunku obserwatora)
• Uwzględnia się fakt istnienia światła rozproszonego.

Generalnie, cechą odbicia dyfuzyjnego jest to, że światło odbija się od powierzchni obiektu we wszystkich kierunkach jednakowo, a intensywność odbitego światła zależy od kąta między padającym promieniem a wektorem normalnym do powierzchni w rozpatrywanym punkcie. Przy założeniach przyjętych przez Phonga oznacza to, że intensywność odbitego światła można obliczać korzystając z zależności kosinusowej (tak jak to było przy cieniowaniu płaskim) (por. rys.VIII.4a).

W przypadku odbicia zwierciadlanego klasycznie kąt między wektorem normalnym do powierzchni a promieniem odbitym jest równy kątowi między wektorem normalnym a w promieniem padającym. Phong uwzględnił jednak fakt, że niektóre powierzchnie nie muszą być perfekcyjnie zwierciadlane - w rzeczywistości występują również powierzchnie błyszczące. W kontekście takich powierzchni Phong dopuścił odchylenie rzeczywistego kierunku obserwacji punktu odbicia od teoretycznego kierunku promienia odbitego (por. kąt β na rysunku VIII.4b). W obliczeniach faktycznie uwzględnia się n-tą potęgę kosinusa kąta β. Wartość n dobiera się eksperymentalnie z uwzględnieniem właściwości materiału powierzchni odbijającej.

Rys.VIII.4. Ilustracja do sposobu obliczania jasności punktu w przestrzeni 3D. a) Wpływ oświetlenia przez punktowe źródło światła, b) efekt odbicia zwierciadlanego

Zwróćmy uwagę, że zarówno dla obliczeń związanych z odbiciem dyfuzyjnym, jak i z odbiciem zwierciadlanym konieczna jest znajomość wektora normalnego N do powierzchni w analizowanym punkcie. Jeżeli analizowany punkt jest wierzchołkiem siatki trójkątnej przybliżającej powierzchnię boczną, to wektor normalny oblicza się jako wektor wypadkowy wektorów normalnych do ścianek trójkątów, przesuniętych do wspólnego wierzchołka. Ponadto istotna jest znajomość wektora L skierowanego z tego punktu do źródła światła.

Podstawowe równanie Phonga ma następującą postać:

$$I=k_aI_a+k_dI_d\cosα+k_sI_s\cos^nβ$$

W równaniu uwzględnione są trzy czynniki mające wpływ na jasność punktu powierzchni: światło rozproszenia ($I_a$), światło odbijane dyfuzyjnie ($I_d$) i światło odbijane zwierciadlanie ($I_s$).

W równaniu tym, współczynniki $k_a$, $k_d$ oraz $k_s$ są współczynnikami wagowymi o wartościach z przedziału od 0 do 1. Współczynniki te umożliwiają regulowanie stopnia wpływu poszczególnych źródeł światła, a pośrednio modelowanie rodzaju materiału, z którego jest wykonana powierzchnia.

W przypadku gdy w scenie występuje większa liczba źródeł światła sumuje się ich wpływ na jasność punktu (należy zwracać uwagę na to żeby nie przekroczyć dopuszczalnej wartości jasności). W przypadku świateł barwnych można korzystać z równania Phonga niezależnie dla każdej składowej R, G i B.

Zaawansowane metody cieniowania

W opisanych dotychczas metodach cieniowania rozpatrywane były tylko promienie docierające do cieniowanej powierzchni bezpośrednio z poszczególnych źródeł światła. Pomijany więc był fakt, że w rzeczywistości światło może dochodzić do powierzchni również po wielokrotnych odbiciach od innych obiektów. Przy uwzględnieniu tego faktu w grafice operuje się pojęciem oświetlenia globalnego.

Pełna realizacja koncepcji oświetlenia globalnego praktycznie nie jest możliwa. Stąd, opracowano kilka metod umożliwiających realizację tej koncepcji w sposób przybliżony. Jedną z tych metod jest omówiona wcześniej metoda śledzenia promieni, w której przy wyznaczaniu barwy określonego punktu powierzchni obiektu uwzględnia się wpływ oświetlenia pochodzącego od obiektów, które znajdowały się na ścieżkach drzewa rozchodzenia się promieni. Zwróćmy dodatkowo uwagę na to, że koncepcja oświetlenia globalnego eliminuje potrzebę korzystania z pomocniczego światła rozproszenia.

Drugim elementem, który ma istotne znaczenie dla zaawansowanych metod cieniowania jest konieczność uwzględnienia szeroko rozumianego pojęcia interakcja światło - materiał. W istocie chodzi o to żeby dokładniej uwzględnić sposób odbijania się światła od różnych materiałów z jakich mogą być wykonane powierzchnie obiektów.

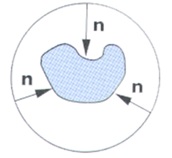
Z punktu widzenia właściwości odbijania światła, powierzchnie obiektów mogą być różnego typu. Mogą to być powierzchnie: gładkie, nierównej, matowe, zwierciadlane, błyszczące, półprzezroczyste, pochłaniające, emisyjne. Na przykład, światło inaczej odbija się od powierzchni gładkiej a inaczej od powierzchni nierównej (por. rys. VIII.5) - istotne są kierunki wektorów normalnych w poszczególnych punktach powierzchni.

Rys. VIII.5. Przykładowe kierunki odbicia światła od nierównej powierzchni

W porównaniu z uproszczonym modelem odbicia dyfuzyjnego w równaniu Phonga, w rzeczywistości światło padające na punkt powierzchni dociera ze wszystkich możliwych kierunków ω_i i jest rozpraszane w różnych kierunkach ω_o niekoniecznie równomiernie.

Sposób odbijania światła od powierzchni wykonanej z określonego materiału jest opisywany za pomocą funkcji BRDF (Bidirectional Reflectance Distribbution Function). Funkcja taka określa jaka część światła padającego z kierunków ω_i jest odbijana w każdym z kierunków wyjściowych ω_o.

Funkcje BRDF mogą być wyznaczane teoretycznie na gruncie fizyki, albo doświadczalnie w wyniku pomiarów. W grafice komputerowej najczęściej wykorzystuje się funkcje uproszczone opracowane przez różnych badaczy na potrzeby symulacji efektów odbicia światła dla różnych materiałów. Można tu wymienić funkcje (modele) Blinna-Phonga, Cooka-Torrance’a, Warda, Orena-Nayara.

Powyższe funkcje są wykorzystywane przy bezpośrednich odbiciach światła od powierzchni obiektu. W grafice komputerowej uwzględnia się również sytuacje, kiedy światło nie tylko odbija się od powierzchni, ale również wnika pod powierzchnię i po kilku wewnętrznych odbiciach jest emitowane na zewnątrz (rys. VIII.6). Takie sytuacje opisują funkcje BSRDF (BSSRDF). Są one wykorzystywane na przykład przy modelowaniu skóry człowieka.

Rys. VIII.6. Ilustracja odbicia podpowierzchniowego