Przechowywanie obrazów

Kompresja bezstratna

Bodaj najprostszą metodą kompresji bezstratnej jest metoda kodowania ciągów znana pod nazwą metoda RLE. Istota tej metody polega na wyszukiwaniu ciągów identycznych elementów i zapamiętywaniu wartości tych elementów i liczby ich powtórzeń. Załóżmy, że piksele w obrazie monochromatycznym (z odcieniami szarości) są reprezentowane za pomocą bajtów i że pewien ciąg pikseli w obrazie jest jak na rysunku XI.1a. Ten ciąg można zapisać krócej, zgodnie z podaną zasadą, tak jak na rys. XI.1b. W każdej parze liczb, pierwsza oznacza liczbę powtórzeń a druga wartość piksela. Oczywiście, mając skompresowany ciąg i pamiętając zasadę kompresji, można łatwo dokonać dekompresji i odtworzyć dokładnie pierwotny ciąg pikseli.

Rys. XI.1. Przykład kompresji metodą RLE. a) Informacja przed kompresją, b) informacja po kompresji

Skuteczność kompresji RLE jest duża wtedy, gdy występują długie ciągi takich samych wartości. Jeżeli jednak pojawiają się pojedyncze wartości, to zamiast zysku może wystąpić strata. (W niektórych implementacjach stosuje się rozwiązania zwiększające efektywność w takich przypadkach.) Najczęściej, w konkretnych implementacjach, kompresji RLE poddawane są poszczególne wiersze obrazu. Nie jest to jednak regułą. Można spotkać rozwiązania, w których kodowane są kolumny obrazu albo ciągi pikseli wybieranych metodą ZigZag (por. rys. XI.4).

Zwróćmy uwagę na pewien problem związany z kodowaniem obrazów barwnych. Jeżeli każdy piksel jest reprezentowany za pomocą trzech składowych RGB, to obraz może być zapisany jako ciąg trójek RGB reprezentujących kolejne piksele albo za pomocą trzech ciągów zawierających odpowiednio tylko składowe R, tylko składowe B, tylko składowe C kolejnych pikseli (por. rysunek XI.2). Można zauważyć, że w tym drugim przypadku efektywność kompresji może być większa, co wynika stąd, że szansa na pojawianie się dłuższych ciągów identycznych wartości jest większa w obrębie ciągu tych samych składowych (tworzących tak zwane płaszczyzny odpowiednio R, G i B).

Rys. XI.2. Wpływ uporządkowania danych na efektywność kompresji. a) Uporządkowanie pikselowe, b) uporządkowanie według składowych barwy

Ogólnie, metoda kompresji RLE pozwala uzyskiwać stopnie kompresji na poziomie 2 : 1, 3 : 1. Oczywiście stopień kompresji zależy od konkretnego obrazu - dla jednych obrazów można uzyskać większy stopień kompresji, dla innych mniejszy. Dodajmy, że jest to cecha charakterystyczna każdej metody kompresji.

Spośród innych metod kompresji bezstratnych stosowanych w praktyce należy wymienić metodę Huffmana, w której stosuje się kody o zmiennej długości. Pikselom, które występują częściej w danym obrazie, przyporządkowuje się krótsze kody.

Działanie metody jest następujące. Na początku sprawdza się ile pikseli w obrazie ma określoną barwę (na przykład poprzez wyznaczenie histogramu obrazu). Procentowy udział poszczególnych barw jest porządkowany od wartości największej do wartości najmniejszej. Następnie tworzy się pomocnicze drzewo .Wśród uporządkowanych procentowych udziałów barw znajduje się te dwie wartości których suma jest najmniejsza. Wartości te łączy się ze sobą a powstałemu węzłowi drzewa przypisuje się znalezioną sumę - wartości składające się na tę sumę są usuwane. Procedurę powtarza się dla pozostałego zbioru wartości. Tworzenie drzewa kończy się po dojściu do korzenia. Po utworzeniu drzewa, w każdym węźle drzewa krawędziom przypisuje się wartości odpowiednio 1 i 0. Następnie, startując z korzenia drzewa, wyznacza się najkrótsze ścieżki prowadzące do liści drzewa. Dla każdej ścieżki rejestruje się wartości przypisane przechodzonym krawędziom. Otrzymane ciągi wartości są kodami, które w procesie kompresji będą przypisywane pikselom o barwach związanych z odpowiednim liściem drzewa.

Proces kompresji polega na tym, że przeglądając kolejne piksele obrazu przypisuje się im nowe kody i dopisuje do tworzonego skompresowanego ciągu. Zauważmy, że w większości przypadków pierwotny kod piksela (na przykład ośmiobitowy) zostaje zastąpiony krótszym kodem. Ważne jest to, że pikselom o najczęściej występujących barwach zastają przypisywane najkrótsze kody. Do wynikowego skompresowanego ciągu koniecznie trzeba dołączyć tabelę kodowania.

Proces dekompresji jest prosty. Przeglądając ciąg skompresowany od początku, sprawdzamy czy napotkana sekwencja bitów odpowiada któremuś kodowi w tabeli kodów. Jeżeli tak, to w odtwarzanym obrazie umieszczamy pierwotny kod piksela przed kompresją. Procedurę powtarza się aż do chwili odzyskania pierwotnego obrazu. W całym procesie kompresja - dekompresja nie jest usuwana żadna informacja. Uzyskiwane stopnie kompresji są na poziomie kilka do jednego.

Przykład

Wykonać kompresję metodą Huffmana obrazu pokazanego na rysunku. Kody pikseli są 8. bitowe.

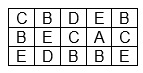
Zaczynamy od wyznaczenia histogramu obrazu.

Z kolei tworzymy drzewo Huffmana i znajdujemy nowe kody dla poszczególnych pikseli.

Następnie wyznaczamy skompresowaną postać obrazu i dołączamy do niej tabelę kodowania

011110110111110010000110001101110
A-000, B-11,C-01,D-001,E-10

Uwaga. W tym prostym przykładzie uzyskany współczynnik kompresji jest niewielki - bez uwzględnienia tabeli kodowania wynosi ok. 2.

Spośród innych metod kompresji bezstratnej należy wymienić metodę słownikową LZW. Istotną cechą tej metody jest to, że w czasie kompresji obrazu jest równocześnie zapisywana informacja o słowniku i nie potrzeba go niezależnie dołączać do postaci skompresowanej. Słownik ten jest odtwarzany stopniowo czasie dekompresji. Ponieważ metoda LZW była przez wiele lat objęta ochroną patentową, to często wykorzystywano w praktyce wcześniejszą wersję tej metody LZ77, która nie była objęta ochroną patentową.

Kompresja stratna

Jedną z najczęściej stosowanych metod kompresji stratnych jest metoda JPEG. Ze względu na złożoność metody ograniczymy się do przedstawienia ogólnej koncepcji tej metody. Na początku, obraz jest dzielony na podobrazy (bloki) o rozmiarach 8x8 pikseli. Procesowi kompresji jest poddawany każdy blok niezależnie. Proces ten obejmuje kroki pokazane na rysunku XI.3.

Rys. XI.3. Schemat blokowy metody kompresji JPEG

W pierwszym kroku wykonuje się konwersję z modelu RGB do modelu YCbCr (cyfrowa wersja modelu YUV). Następne kroki algorytmu wykonuje się niezależnie dla składowej Y i dla składowych chrominancji Cb oraz Cr. Obliczenia związane ze składową Y są robione z większą dokładnością niż dla składowych Cb, Cr - wykorzystuje się tu fakt, iż oko człowieka jest bardziej czułe na zmiany jasności niż na zmiany barwy.

Dla tablicy wartości (np. Y) o rozmiarze 8×8 jest wykonywana transformacja kosinusowa i w efekcie uzyskuje się nowy zestaw 64 liczb - współczynników z rozwinięcia kosinusowego. Wykorzystuje się tu następującą zależność

$$S_{vu}=1/4C_uC_v∑↙{x=0}↖7∑↙{y=0}↖7 s_{yx}\cos{(2x+1)uπ}/16\cos{(2y+1)vπ}/16$$

gdzie $s_{yx}$ są to oryginalne dane z tablicy o współrzędnych yx a $S_{vu}$ są to współczynniki uzyskane w wyniku transformacji kosinusowej, zapisywane w tablicy o współrzędnych vu. Współczynniki $C_u$ i $C_v$ są równe $1/√2$ gdy $u,v=0$ i równe 1 w przeciwnym przypadku.

W kolejnym kroku wykonywana jest tak zwana kwantyzacja. Jej celem jest zamienienie możliwie dużej liczby współczynników transformaty na zera. Generalnie chodzi o to, że wśród współczynników transformaty są takie, które niosą dużą ilość informacji o obrazie i takie, które niosą niewielką ilość informacji o obrazie. Te ostatnie można wyeliminować bez większej straty dla ogólnej jakości obrazu - ich wpływ jest na tyle mały, że obserwator może nie zauważyć zmian w obrazie związanych z ich usunięciem.

Kwantyzację realizuje się w następujący sposób. Korzystamy z pomocniczej tablicy 8×8, zawierającej odpowiednio dobrane wartości. Kolejno dzieli się przez siebie współczynniki z tablicy uzyskanej w wyniku transformacji, przez odpowiednie współczynniki z pomocniczej tablicy (to znaczy, pierwszy element tablicy współczynników transformacji dzielimy przez pierwszy element pomocniczej tablicy, potem to samo wykonujemy w stosunku do drugich współczynników itd.) i wyniki zaokrągla się w dół. Elementy pomocniczej tablicy są tak dobrane, żeby w wynikowej tablicy pojawiała się możliwie duża liczba zer zgrupowanych w prawej dolnej części wynikowej tablicy. Dzięki operacji kwantyzacji uzyskuje się kompresję informacji, przy czym jest to operacja nieodwracalna.

Tablica uzyskana w wyniku kwantyzacji jest w ostatnim kroku poddawana kodowaniu metodą RLE i następnie metodą Huffmana. Kodowaniu metodą RLE poddawany jest ciąg wartości z wynikowej tablicy przeglądany w porządku ZigZag, tak jak na rysunku XI.4. Taki porządek jest przyjęty ze względu na to, że pozwala uzyskać długi ciąg zer zgrupowanych w prawej dolnej części tablicy. Zauważmy, że do ciągu nie wchodzi element z lewego górnego rogu oznaczony jako DC. Jest on kodowany wspólnie z odpowiednimi elementami dla innych bloków obrazu 8x8, z których składa się cały obraz poddawany kompresji.

Rys. XI.4. Przeglądanie elementów tablicy w porządku ZigZag

Przy dekompresji obrazu postępuje się w odwrotnej kolejności jak przy kompresji. Najpierw ma miejsce odkodowanie ciągu właściwe dla metody Huffmana, a potem dla metody RLE. Odtworzona tablica jest poddawana odwrotnej operacji jak przy kwantyzacji (z wykorzystaniem tej samej pomocniczej tablicy), z tym, że oczywiście nie można odtworzyć wyzerowanych współczynników. Z kolei, odzyskana tablica współczynników transformaty kosinusowej jest poddawana odwrotnej transformacji kosinusowej. Na końcu następuje konwersja z modelu YCbCr do modelu RGB.

Kompresja metodą JPEG pozwala uzyskiwać stopnie kompresji 20:1 - 30:1, przy praktycznie niezauważalnych zniekształceniach obrazu odzyskiwanego po dekompresji. Przy większych stopniach kompresji zmiany takie są już zauważalne. (Zmianę stopnia kompresji uzyskuje się poprzez zmianę współczynników pomocniczej tablicy wykorzystywanej w czasie kwantyzacji.) Ilustruje to rys. XI.5, na którym obraz Leny został poddany kompresji 20 :1 i 50:1. Obrazy uzyskane po dekompresji są pokazane z prawej strony odpowiednio na górze i na dole. Na obrazie z lewej strony na dole przedstawiono obraz różnicowy między oryginałem a obrazem odzyskanym po dekompresji w stosunku 20:1. Widać tu tę część informacji, która została usunięta w procesie kompresja-dekompresja.

Rys. XI.5. a) Obraz Leny, b) obraz po kompresji 20:1 i po dekompresji, c) obraz różnicowy między obrazami a) i b), d) obraz po kompresji 50:1 i dekompresji

Wyżej przedstawiona została podstawowa wersja standardu JPEG najczęściej stosowana w praktyce. Faktycznie, pełny standard obejmuje 29 różnych kompresji, w tym również kompresję bezstratną. W 2000 roku został opracowany kolejny wariant kompresji JPEG 2000, w którym założono, że kompresja jest wykonywana bezpośrednio na całym obrazie oraz wykorzystano transformatę falkową. Jednak ten standard nie przyjął się w praktyce.

Na zakończenie dodajmy, że omówione wyżej metody kompresji są stosowane do kompresji pojedynczych obrazów. Przy kompresji sekwencji obrazów są stosowane inne metody, na przykład takie jak w standardach MPEG.