Algorytmy rasteryzacji

Odcinki

Zacznijmy od przedstawienia problemu. Zadanie polega na narysowaniu odcinka o znanych współrzędnych początku i końca. Na rysunku IV.1a pokazano wygląd odcinka do jakiego jesteśmy przyzwyczajeni i jaki możemy uzyskać na papierze, korzystając z ołówka i linijki. Na rysunku IV.1b pokazano wygląd tego samego odcinka narysowanego na bazie rastra. W tym przykładzie specjalnie została wybrana bardzo mała rozdzielczość rastra, po to żeby dobrze pokazać problem. Ponadto, wybór pikseli wchodzących w skład odcinka był dość arbitralny.

Rys. IV.1. a) Idealny wygląd odcinka; b) odcinek narysowany na rastrze

Zastanówmy się wobec tego nad algorytmem, który umożliwi wybieranie pikseli dla odcinka o zadanych współrzędnych początku i końca. Przyjmijmy, że z naszym rastrem związany jest układ współrzędnych x, y. Wiadomo, że jeżeli znane są współrzędne końców odcinka, to można znaleźć równanie prostej, na której ten odcinek leży. Pamiętamy, że równanie takie ma postać

$$y=mx+b$$

gdzie m jest współczynnikiem określającym nachylenie prostej i $m=tgα$ a α jest kątem nachylenia prostej. Znając równanie prostej możemy dalej postępować następująco. Dla kolejnej kolumny rastra o współrzędnej $x_i$ można wyznaczyć z równania prostej wartość współrzędnej $y_i$ punktu leżącego na prostej. Następnie można znaleźć najbliższy punkt rastra w kolumnie $x_i$. Wyjaśnia to rysunek IV.2. Procedurę należy powtarzać dla każdej kolumny w zakresie zmian współrzędnej x dla odcinka.

Rys. IV.2. Wyznaczanie kolejnych pikseli przy korzystaniu z równania linii

Metoda jest prosta. Jednak dla wyznaczenia kolejnego piksela trzeba wykonać operacje mnożenia, dodawania i zaokrąglenia. Liczbę wykonywanych operacji można zmniejszyć jeżeli zauważy się, że przy stałym nachyleniu linii i stałym odstępie między kolumnami pikseli równym 1, wartość $y_{i+1}$ w kolejnej kolumnie $x_{i+1}$ można obliczyć dodając do wartości $y_i$ stały przyrost $Δy=m$. Korzystając z zależności

$$y_{i+1}=y_i+m$$

dla obliczenia kolejnego piksela trzeba wykonać jedno dodawanie zmiennopozycyjne i zaokrąglenie. Oszczędzamy wobec tego jedno mnożenie. Jeżeli weźmiemy pod uwagę, że przy tworzeniu jednego obrazu trzeba często narysować kilkadziesiąt odcinków i dla każdego z nich trzeba obliczyć kilkadziesiąt pikseli, to okaże się, że oszczędność w sensie liczby wykonywanych obliczeń staje się znacząca. A pamiętamy, że czas jaki mamy na obliczenie kolejnego obrazu jest zawsze bardzo krótki. Algorytm w przedstawionej wersji jest określany jako algorytm DDA.

Zauważmy, że opisany sposób postępowania jest słuszny przy założeniu, że nachylenie odcinka jest mniejsze od 45°. Przy kątach większych od 45° i mniejszych od 90° trzeba wprowadzić modyfikację polegającą na tym, że teraz wyznaczane będą piksele w kolejnych wierszach, a nie w kolejnych kolumnach, tak jak poprzednio. Gdyby tej zmiany nie wprowadzić liczba pikseli tworzących odcinek mogłaby być zbyt mała. Ilustruje to rysunek IV.3.

Rys. IV.3. Odcinek o nachyleniu większym od 45°. a) Zestaw pikseli przy wybieraniu według kolumn - wariant niepoprawny. b) Zestaw pikseli przy wybieraniu według wierszy – wariant poprawny

Okazuje się, że można jeszcze zmniejszyć czas obliczeń przy rysowaniu odcinka dodając wymóg, by wykonywane były tylko obliczenia stałopozycyjne, a nie zmiennopozycyjne jak to ma miejsce w algorytmie DDA. Odpowiedni algorytm został opracowany przez Bresenhama.

Zanim podamy pełny algorytm Bresenhama spróbujmy zobaczyć jak wyglądało rozumowanie, które doprowadziło do końcowej postaci algorytmu. Zakładamy, że nachylenie odcinka jest mniejsze od 45° (czyli $0<m<1$). Załóżmy, że został już znaleziony piksel w kolumnie $x_i$ mamy znaleźć piksel w następnej kolumnie $x_{i+1}$. Można zauważyć, że wybór ogranicza się tylko do dwóch pikseli: tego leżącego w tym samym wierszu i tego w wierszu powyżej (zobacz rysunek IV.4.). Pozostaje więc znalezienie prostego kryterium, które pozwoli wybrać piksel przy jak najmniejszym nakładzie obliczeniowym. Bresenham zaproponował, żeby takie kryterium skonstruować wykorzystując różnicę odległości D1 i D2 rozważanych pikseli od punktu leżącego na rzeczywistym odcinku (por. rysunek IV.4). Można zauważyć, że badając znak różnicy (D1 – D2) można wybrać piksel. Przy znaku minus będzie to górny piksel, przy znaku plus dolny piksel.

Rys. IV.4. Ilustracja toku rozumowania Bresenhama. Na zielono zaznaczono piksele między którymi należy dokonać wyboru w kolejnej kolumnie

Ostatecznie algorytm podany przez Bresenhama ma następującą postać.

1. Znając współrzędne końców odcinka należy wybrać koniec odcinka o mniejszej współrzędnej x. (Ponieważ algorytm nie zawsze daje ten sam wynik przy rozpoczynaniu od różnych końców odcinka, przyjęto za zasadę, że zawsze zaczyna się od tego końca, dla którego współrzędna x jest mniejsza). Wybrany punkt $(x_1,\,y_1)$ jest pierwszym punktem rysowanego odcinka.
2. Obliczyć pomocnicze wielkości:

   

   oraz wartość początkową parametru decyzyjnego jako

   

3. Dla kolejnych kolumn o współrzędnych $x_k$, zaczynając od $k=0$ należy sprawdzić znak wartości pomocniczego parametru $p_k$.

   W przypadku gdy $p_k<0$ następny piksel ma współrzędne $(x_{k+1}, y_k)$ i nowa wartość parametru decyzyjnego jest określana z zależności $p_{k+1}=p_k+a$.

   W przeciwnym przypadku następny punkt ma współrzędne $(x_{k+1}, y_{k+1})$ i nowa wartość parametru decyzyjnego jest określana z zależności $p_{k+1}=p_k+b.$

4. Krok 3 jest powtarzany dopóki nie dojdziemy do końca odcinka.

Zauważmy, że w każdym kroku, w celu wyznaczenia kolejnego piksela musimy wykonać tylko jedno dodawanie stałopozycyjne.

Przykład

Korzystając z metody Bresenhama znaleźć kolejne piksele dla odcinka o współrzędnych końców (2,2), (8,5).

1. Wybieramy pierwszy punkt odcinka. Jest to punkt (2,2).
2. Obliczamy pomocnicze wielkości $$\table Δx=8-2=6, Δy=5-2=3, a=2∗3=6, b=6-12=-6$$ $$p_0=2Δy-Δx=6-6=0$$

3. Wyznaczamy kolejne piksele.

   Ponieważ $p_0=0$, to następny piksel ma współrzędne (3,3) i $p_1=p_0+b=0-6=-6$

   Ponieważ $p_1<0$, to następny piksel ma współrzędne (4,3) i $p_2=p_1+a=-6+6=0$

   Ponieważ $p_2=0$, to następny piksel ma współrzędne (5,4) i $p_3=p_2+b=0-6=-6$

   itd. Cały odcinek pokazano na rysunku IV.5.

Rys. IV.5. Przykład działania algorytmu Bresenhama

Aliasing

Wygląd odcinka narysowanego na rastrze z pewnością nie jest najlepszy. Przy niezbyt dużej rozdzielczości rastra wyraźnie widać, że kształt odcinka odbiega od idealnego – widać tzw. efekt schodkowy. Sytuacja staje się jeszcze mniej korzystna jeżeli odcinek będzie obracał się względem jakiegoś punktu. W trakcie zmieniania nachylenia odcinka zmienia się wzór ułożenia pikseli. Na rysunku IV.6 pokazano kilka przykładów odcinków o różnych nachyleniach.

Rys. IV.6. Przykłady wyglądu odcinka przy różnych kątach nachylenia

Opisywany efekt określany jest mianem aliasingu. Jest on skutkiem skończonej rozdzielczości rastra z jakim mamy do czynienia. Efekt ten nie może być usunięty żadną metodą. Można jednak próbować go zmniejszać. Metody służące temu są określane jako metody antyaliasingowe.

Narzucającym się rozwiązaniem jest zwiększanie rozdzielczości. Tendencja do zwiększania rozdzielczości monitorów utrzymuje się od lat i obecnie efekty aliasingu są coraz mniej zauważalne. Jednak mimo, że często nie zauważamy efektu aliasingu to on istnieje i można się o tym przekonać powiększając obraz widziany na ekranie monitora, na przykład w czasie projekcji na dużym ekranie ściennym. Efekt ten ilustruje rysunek IV.7, na którym pokazano z lewej strony odcinek tak jak go widać na ekranie monitora a z prawej strony powiększony fragment odcinka, na którym widać strukturę pikselową odcinka, w stosunku do którego zastosowana już została pewna metoda antyaliasingowa. Przyglądając się powiększonej wersji odcinka można zauważyć, że poszczególne piksele mają różne odcienie szarości.

Rys. IV.7. a) Odcinek; b) fragment odcinka w powiększeniu

Idea zastosowanej metody polega na tym, że w każdej kolumnie wybiera się dwa piksele, leżące najbliżej punktu na idealnym odcinku. Zależnie od odległości pikseli od punktu na odcinku określa się odcienie szarości tych pikseli – im piksel jest bliżej punktu na odcinku tym jest ciemniejszy. Suma odcieni szarości obu pikseli jest stała. W szczególnym przypadku, gdy jeden piksel leży dostatecznie blisko punktu na odcinku, w kolumnie jest wyświetlany jeden piksel. Omawiany sposób zilustrowano na rysunku IV.8.

Rys. IV.8. Ilustracja metody zmniejszania efektu aliasingu, w której w każdej kolumnie są wyświetlane dwa piksele

Metody antyaliasingowe mogą być wykorzystywane bezpośrednio w czasie rasteryzacji konturów obiektów. W praktyce często korzysta się z innego rozwiązania, tzw. antyalisingu pełnoekranowego. Polega to na tym, że dopiero po wygenerowaniu obrazu pikselowego korzysta się z metody antyaliasingu w odniesieniu do całego obrazu. Typowo jest to metoda FSAA. Polega ona na tym, że obraz jest generowany w większej rozdzielczości niż docelowa a przy przejściu do rozdzielczości docelowej następuje uśrednianie barw sąsiednich pikseli.

Okrąg

Zastanówmy się teraz jak można narysować okrąg o środku w początku układu współrzędnych i o promieniu r. Oczywiście można by skorzystać z równania okręgu $x^2+y^2=r^2$ i dla kolejnych wartości $x_i$ wyznaczać w każdej kolumnie wartości y i po zaokrągleniu znajdować odpowiednie piksele. Metoda taka jest jednak kosztowna obliczeniowo (występuje między innymi podnoszenie do kwadratu oraz pierwiastkowanie). Ponadto rozmieszczenie pikseli przybliżających okrąg nie jest równomierne wzdłuż okręgu (proszę się zastanowić dlaczego). Stąd, w praktyce są stosowane inne metody. Niżej przedstawiono metodę z punktem środkowym (metoda mid point).

Przede wszystkim można zauważyć, że przy wyznaczaniu pikseli przybliżających okrąg można wykorzystać właściwość symetrii okręgu. Pozwala to na ograniczenie obliczania pikseli tylko do jednego oktantu (jednej ósmej) okręgu a pozostałe piksele znajdować zgodnie z zasadą pokazaną na rysunku IV.9.

Rys. IV.9. Po wyznaczeniu punktu zaznaczonego na czerwono, punkty zaznaczone na zielono są wyznaczane przy wykorzystaniu właściwości symetrii okręgu

Wyjaśnijmy teraz na czym polega pomysł metody z punktem środkowym. Przede wszystkim przypomnijmy, że dla każdego punktu leżącego na okręgu spełnione jest równanie $x^2+y^2-r^2=0$. Dla punktu leżącego na zewnątrz okręgu spełniona jest nierówność $x^2+y^2-r^2>0$, a dla punktu leżącego wewnątrz okręgu spełniona jest nierówność $x^2+y^2-r^2<0$. Z kolei, jeżeli ograniczymy się do pierwszego oktantu okręgu, to po wyznaczeniu piksela dla kolumny $x_i$, w następnej kolumnie $x_{i+1}$ możemy ograniczyć się tylko do wyboru między dwoma pikselami: pikselem leżącym w tym samym wierszu i pikselem leżącym w wierszu poniżej (por. rysunek IV.10). Wyboru między tymi dwoma pikselami można dokonać analizując położenie względem okręgu punktu znajdującego się w połowie odcinka łączącego dwa rozważane piksele, tak zwanego punktu środkowego. Zależnie od tego czy punkt środkowy leży wewnątrz okręgu czy na zewnątrz okręgu, należy wybrać odpowiednio górny albo dolny piksel. Okazało się, że w przypadku problemu rysowania okręgu, podobnie jak w przypadku rysowania odcinka metodą Bresenhama, można znaleźć kryterium wyboru piksela w kolejnej kolumnie, wymagające wykonania jedynie kilku prostych operacji.

Rys. IV.10. Ilustracja metody z punktem środkowym

Ostatecznie, algorytm rysowania okręgu o środku w początku układu współrzędnych i o promieniu r metodą z punktem środkowym wygląda następująco.

1. Punkt początkowy ma współrzędne (0, r). Natomiast początkowa wartość pomocniczego parametru decyzyjnego wynosi $p_0=5/4-r$

2. Dla kolejnych kolumn o współrzędnych $x_k$, zaczynając od k = 0, należy sprawdzić znak wartości pomocniczego parametru $p_k$.

   W przypadku gdy $p_k<0$, następny piksel ma współrzędne $(x_{k+1}, y_k)$ i nowa wartość parametru decyzyjnego jest określana z zależności $$p_{k+1}=p_k+2x_{k+1}+1.$$

   W przeciwnym przypadku, następny punkt ma współrzędne $(x_{k+1}, y_{k-1})$ i nowa wartość parametru decyzyjnego jest określana z zależności $$p_{k+1}=p_k+2x_{k+1}+1–2y_{k+1}.$$

3. Wyznaczyć siedem pikseli o współrzędnych wynikających z właściwości symetrii okręgu.

4. Powtarzać kroki 2 i 3 do czasu gdy spełniony będzie warunek $x=y$.

Proponuję samodzielne wyznaczenie pikseli dla okręgu o środku w początku układu współrzędnych i o promieniu $r=20$.

Inne krzywe i figury

Mając do dyspozycji algorytm rysowania odcinka można rozwiązać problem rysowania linii łamanych i wielokątów. Na rysunku IV.11 pokazano przykłady takich obiektów. Zauważmy, że liniom i konturom figur można przypisywać różne atrybuty, takie jak styl (linia ciągła, przerywana, kropkowana itp.), grubość czy kolor.

Rys. IV.11. Przykłady obiektów budowanych z odcinków, którym przypisano różne atrybuty

Tak proste obliczeniowo algorytmy jak dla odcinka i okręgu istnieją dla niewielu innych obiektów (na przykład dla elipsy). W przypadku innych krzywych opisanych równaniami, na ogół konieczne jest korzystanie z równania krzywej i wyznaczania wartości współrzędnej y dla kolejnych wartości współrzędnej x i zaokrąglania do najbliższego piksela. W niektórych przypadkach można korzystać z właściwości symetrii (na przykład dla krzywej sinusoidalnej).

Często jednak nie znamy równania krzywej, która jest nam potrzebna. Wtedy pozostaje interakcyjne narysowanie takiej krzywej. Nie zawsze jest to wygodny sposób. W takich przypadkach można skorzystać z krzywych wielomianowych specjalnego typu, na przykład z krzywych Béziera (por. następny wykład).

Rasteryzacja wnętrz domkniętych konturów

Domknięte kontury wymagają często wyznaczania pikseli należących do wnętrz konturów. Wyróżnić tu można dwa sposoby realizacji takiej rasteryzacji: przeglądanie wierszami (ang. scan line) i z punktem początkowym (ang. seed).

Metoda przeglądania wierszami

W metodach przeglądania wierszami zakłada się, że znane są równania opisujące kontur. W metodach tych występują dwie fazy. W pierwszej fazie, dla każdego wiersza rastra znajduje się przecięcia wiersza z konturami obiektów i ustala się pary punktów przecięć, między którymi należy dokonać wypełnienia. W drugiej fazie ma miejsce wypełnianie odcinków wyznaczonych w pierwszej fazie. Na rysunku IV.12 pokazano przykładowe linie rastra przecinające wielokąt i zaznaczono punkty przecięć z krawędziami wielokąta. W drugiej fazie zostaną wypełnione odcinki ograniczone przez pary punktów P₁ (1,2), P₂ (3,4), P₃ (5,6).

Rys. IV.12. Wyznaczanie odcinków należących do wnętrza wielokąta, które w drugiej fazie algorytmu przeglądania wierszami zostaną wypełnione

Algorytm koncepcyjnie jest prosty i nie stwarza istotnych problemów implementacyjnych w przypadku wielokątów wypukłych. Przy konkretnej implementacji, dla ustalonej klasy obiektów, na przykład dla wielokątów niewypukłych, trzeba zwracać uwagę na wierzchołki. Na ogół konieczne jest wyróżnienie dwóch klas wierzchołków: takich, dla których dwie stykające się w wierzchołku krawędzie leżą po jednej stronie linii rastra (inaczej mówiąc są to wierzchołki, w których występuje lokalne ekstremum) i takie, dla których krawędzie leżą po obu stronach linii rastra (por. rysunek IV.13).

Rys. IV.13. Dwa rodzaje wierzchołków

Metoda z punktem początkowym

W grupie metod z punktem początkowym zakłada się, że na ekranie narysowany jest kontur zamknięty oraz, że znany jest punkt należący do wnętrz konturu. Wypełnianie zaczyna się od znanego punktu należącego do wnętrza figury.

Przykładowa kolejność postępowania może być następująca. Od punktu początkowego poruszamy się w lewo wzdłuż wiersza rastra aż do napotkania brzegu obszaru. Następnie w tym samym wierszu poruszamy się w prawo od punktu początkowego aż do napotkania brzegu obszaru. Z kolei przechodzimy do sąsiedniego wiersza i powtarzamy procedurę, zaczynając od punktu leżącego nad punktem początkowym. Powtarzamy to dopóki jest to możliwe. Następnie przechodzimy do wiersza znajdującego się poniżej wiersza, w którym leży punkt początkowy i postępujemy podobnie jak poprzednio. Jeżeli dodatkowo cały czas tworzona jest i aktualizowana lista aktywnych pikseli – tych, które leżą na obrzeżu już wypełnionego obszaru, to w razie potrzeby próbujemy kontynuować procedurę od pierwszego piksela znalezionego na liści aktywnych pikseli itd.

Na rysunku IV.14 zilustrowano opisany sposób postępowania, pokazując pewien pośredni stan realizacji wypełniania. Na niebiesko zaznaczono punkt początkowy. Czarnym kolorem zaznaczono już znalezione piksele należące do wnętrza konturu, Zielonym kolorem wyróżniono piksele znajdujące się na liście aktywnych pikseli.

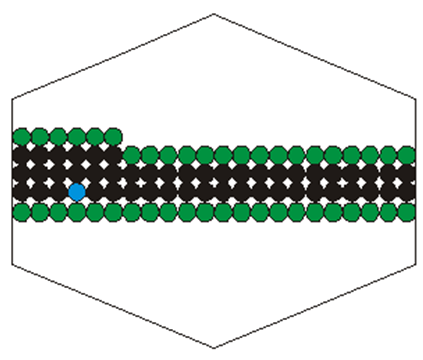
Rys. IV.14. Ilustracja metody wypełniania z punktem początkowym. Wypełnianie od punktu zaznaczonego na niebiesko

Zauważmy, że algorytm może wypełniać kontury zarówno wypukłe jak i niewypukłe a nawet niespójne.

Rasteryzacja trójkąta

Szczególnym przypadkiem wypełniania jest rasteryzacja trójkąta o znanych wierzchołkach. Można ją oczywiście wykonać jedną z omówionych wyżej metod.

W praktyce często wykorzystuje się tzw. współrzędne barycentryczne. (p. niżej). Jeżeli dla konkretnego piksela wyznaczy się współrzędne barycentryczne, to badając znaki tych współrzędnych można stwierdzić czy piksel należy do wnętrza trójkąta (gdy wszystkie współrzędne są dodatnie) czy też nie należy do wnętrza (przynajmniej jedna współrzędna jest ujemna).

Współrzędne barycentryczne

Współrzędne barycentryczne opisują położenie punktu w trójkącie o znanych współrzędnych wierzchołków (rys. IV.15).

Rys. IV.15. Przykładowy trójkąt z wyróżnionym punktem wewnętrznym

Załóżmy, że współrzędne wierzchołków trójkąta to odpowiednio A, B, C. Położenie punktu U wewnątrz trójkąta opisują współrzędne α, β, γ spełniające równanie

U = αA + βB + γC

takie, że

α + β + γ = 1   i   α, β, γ≥0

Współrzędne barycentryczne można wykorzystać również do interpolacji liniowej wartości funkcji wewnątrz trójkąta.

Załóżmy, że znane są wartości pewnej funkcji w wierzchołkach trójkąta A,B,C, odpowiednio f(A),f(B),f(C) oraz, że znane są współrzędne barycentryczne punktu U wewnątrz trójkąta. Wtedy wartość funkcji w punkcie U wynosi

$$f(U)=αf(A)+βf(B)+γf(C)$$

Wyznaczanie barw pikseli

Z procesem rasteryzacji wiąże się problem wyznaczania barw pikseli. W przypadku linii czy brzegów konturów najczęściej z góry określa się barwę rysowanej linii i wszystkim pikselom tej linii przypisuje się tę barwę.

W przypadku pikseli należących do wnętrza konturu możliwe są różne warianty wypełniania. Wnętrze może być wypełnione jednolitą barwą (wypełnianie ciągłe), zmienną barwą (wypełnienie tonalne) albo teksturą. Przykłady wypełniania pokazano na rysunku IV.16.

Rys. IV.16. Przykłady wypełniania wnętrza figury: a) jednolitą barwą, b) tonalne, c) teksturą

Przy wypełnianiu jednolitą barwą, wszystkie piksele wnętrza otrzymują z góry przyjętą barwę. Przy wypełnianiu teksturą, pikselom wnętrza przypisuje się barwy „pobierane” odpowiednio z wykorzystywanego wzoru tekstury (problemy związane z teksturowaniem są omawiane w wykładzie VIII). Jeśli chodzi o wypełnianie tonalne, to ograniczymy się tu do przedstawienia metody Gouraud w odniesieniu do trójkąta.

Załóżmy, że znamy barwy (wartości jasności) trzech wierzchołków trójkąta a chcemy znaleźć barwę dla każdego piksela należącego do trójkąta.

Weźmy pod uwagę lewą krawędź trójkąta (por. rysunek IV.17). Oznaczmy wartości jasności barw wierzchołkowych przez I₁ i I₂. Krawędź ta jest przecinana przez linie rastra. Znając wartości I₁ i I₂ możemy dla każdego punktu przecięcia krawędzi z linią rastra znaleźć jasność pośrednią, korzystając z metody interpolacji liniowej. Podobnie, dla prawej krawędzi trójkąta o jasnościach wierzchołkowych I₁ i I₃ możemy znaleźć barwy w punktach pośrednich krawędzi. Z kolei, weźmy pod uwagę fragment wiersza rastra należący do trójkąta. Ponieważ znamy już wartości jasności na końcach tego odcinka (I_a oraz I_b na rysunku IV.17), to możemy podobnie jak poprzednio znaleźć wartości pośrednie dla poszczególnych pikseli należących do odcinka rastra (na przykład wartość I_c na rysunku). Postępując w ten sposób dla innych wierszy rastra możemy znaleźć wartość jasności dla każdego piksela należącego do wnętrza trójkąta. W efekcie, można uzyskać tonalne cieniowanie powierzchni trójkąta. Przykłady takiego cieniowania są pokazane na rysunku IV.17 dla wersji z odcieniami szarości i dla wersji kolorowej.

Rys. IV.17. Metoda Gouraud. a) Ilustracja działania metody, b,c) przykłady uzyskiwanych efektów

Pewnym ograniczeniem metody Gouraud jest to, że zestaw barw jakie można uzyskać wewnątrz wypełnianego trójkąta jest ograniczony przez zestaw barw wierzchołkowych.

Obliczenia związane z metodą Gouraud można wykonać również, korzystając ze współrzędnych barycentrycznych. Jeżeli znane są kolory c₀, c₁, c₂ dla wierzchołków trójkąta, to kolor piksela c_p o współrzędnych barycentrycznych α, β, γ można wyznaczyć z zależności

$$c_p=αc_0+βc_1+γc_2$$