Rendering

Bryła widzenia

Zdefiniowana scena może być obserwowana z różnych punktów. Obserwator może znajdować się w dowolnym miejscu sceny, przy czym na ogół zakłada się, że obserwator jest na zewnątrz poszczególnych obiektów. Ponadto, obserwator może patrzeć w dowolnym kierunku. Zależnie od położenia obserwatora i kierunku patrzenia, na ekranie powinien pokazać się odpowiedni widok sceny. Poglądowo wyjaśnia to rysunek VII.1 (dla uproszczenia pokazano widok z góry). Założono również, że kąt widzenia α; jest dla obserwatora stały.

Rys. VII.1. Położenie obserwatora i kierunek obserwacji określają elementy sceny widoczne dla obserwatora. Zaznaczono dwa przykładowe położenia obserwatora i kierunki patrzenia: A i B

Przy położeniu A obserwatora obiekt 5 nie pojawi się na ekranie, obiekty 1, 2 i 4 będą widoczne jedynie częściowo a obiekt 3 prawdopodobnie nie będzie widoczny, bowiem będzie zasłonięty przez obiekty leżące bliżej obserwatora. Przy położeniu B obserwatora obiekt 5 nie będzie widoczny na ekranie, natomiast wszystkie pozostałe obiekty będą widoczne jedynie częściowo.

Z analizy rysunku można wysnuć kilka wniosków. Nie zawsze wszystkie obiekty znajdujące się w scenie są widoczne. Nie zawsze widoczne są całe obiekty, bowiem albo nie mieszczą się w całości w polu widzenia obserwatora określonym przez kąt α; albo są zasłonięte częściowo przez inne obiekty. Widoczne są tylko przednie części powierzchni bocznych obiektów.

W rzeczywistości, obserwując scenę 3D obserwator powinien zobaczyć na ekranie te elementy, które znajdą się w prawidłowym ostrosłupie czworokątnym, którego wierzchołek znajduje się w „oku” obserwatora O, oś główna ostrosłupa jest prostopadła do płaszczyzny ekranu a kąt rozwarcia ostrosłupa jest określony przez wielkość ekranu i jego odległość od obserwatora. Poglądowo wyjaśnia to rysunek VII.2.

Rys. VII.2. Ostrosłup, w obrębie którego znajdują się obiekty sceny potencjalnie widoczne na ekranie

Teoretycznie wysokość ostrosłupa powinna być nieskończenie długa. W praktyce jednak wprowadza się dodatkowe ograniczenia w postaci płaszczyzn: przedniej i tylnej, które ograniczają ostrosłup do ostrosłupa ściętego. Ograniczenia te wynikają ze względów czysto praktycznych. Nie ma bowiem sensu rozpatrywać obiektów, które znajdują się zbyt daleko od obserwatora i są na przykład zasłonięte albo są zbyt małe. Podobnie nie jest sensowne zajmowanie się obiektami, które na przykład znajdują się po tej stronie ekranu co obserwator i nie powinny pojawić się na ekranie.

Na rysunku VII.3 pokazano widok z boku otrzymanego ostrosłupa ściętego. Ostrosłup ten jest często określany jako bryła widzenia. Bryła widzenia obejmuje więc tę część przestrzeni sceny, która może być widoczna na ekranie. W efekcie, ze względu na szybkość obliczeń sensowne jest rozważanie tylko tych obiektów sceny, które w całości lub przynajmniej częściowo należą do bryły widzenia. Pojawia się więc problem obcinania obiektów sceny przez ściany bryły widzenia.

Rys. VII.3. Widok z boku ostrosłupa ściętego tworzącego bryłę widzenia

Eliminowanie powierzchni niewidocznych

Obserwując dowolny obiekt nieprzezroczysty zawsze widzimy tylko część jego powierzchni bocznej. Musimy oczywiście uwzględnić ten fakt przy wyświetlaniu obiektu na ekranie. Podobnie, wyświetlając kilka obiektów musimy uwzględniać fakt, że jedne obiekty mogą zasłaniać inne. W celu rozwiązania problemu widoczności opracowano różne algorytmy. Niżej przedstawimy dwa algorytmy.

Zacznijmy od najprostszego przypadku kiedy mamy do czynienia z pojedynczą wypukłą bryłą, której powierzchnia boczna jest opisana za pomocą wielokątów. Dla każdego wielokąta można wyróżnić stronę wewnętrzną (widzianą przy obserwacji od strony wnętrza bryły) i stronę zewnętrzną (widzianą przy obserwacji bryły z zewnątrz) i w konsekwencji określić wektor normalny do powierzchni skierowany na zewnątrz bryły. Sprawdzając dla konkretnej ściany bocznej bryły czy jej wektor normalny N (a dokładniej składowa N_z tego wektora) jest skierowany do obserwatora czy w przeciwną stronę, możemy stwierdzić czy ta ściana (wielokąt) jest widoczna. Ilustruje to rysunek VII.4a.

Zwróćmy jeszcze raz uwagę na założenie o wypukłości bryły. W przypadku brył, które nie są wypukłe, algorytm może dawać niepoprawne wyniki. Gdyby w miejscu ostrosłupa z rysunku VII.4a znajdowała się bryła z rysunku VII.4b, to zielona ścianka będzie zakwalifikowana jako widoczna, podczas gdy faktycznie widoczna jest tylko część tej ścianki.

Znajomość wektorów normalnych ścianek powierzchni bocznych obiektów umożliwia również czasami eliminowanie obliczeń związanych z tylnymi (niewidocznymi) ściankami.

Rys. VII.4. Ilustracja do algorytmu określania widoczności ścianek na podstawie analizy wektorów normalnych. a) Przypadek bryły wypukłej, b) przypadek bryły niewypukłej

Inna koncepcja rozwiązywania problemu widoczności jest realizowana w algorytmie z-bufora. Tym razem nie przyjmuje się żadnych założeń co do rodzaju wyświetlanych obiektów ani co do kolejności analizowania obiektów. Widoczność obiektów rozstrzyga się dla każdego piksela obrazu niezależnie. Do realizacji algorytmu potrzebna jest dodatkowa pamięć, tak zwany z-bufor, w której można dla każdego piksela przechowywać wartość współrzędnej z aktualnie najbliższego obiektu dla danego piksela.

Na początku, do pamięci obrazu zapisuje się barwę tła dla wszystkich pikseli obrazu, natomiast w z-buforze zapisuje się największą wartość współrzędnej z jaka może wystąpić w scenie (zakładamy, że oś z jest skierowana od obserwatora w kierunku sceny); w szczególności może to być współrzędna z tylnej ściany bryły widzenia.

Z kolei, jeżeli analizujemy jakiś wielokąt i trafimy na punkt, który potencjalnie znajdzie się w końcowym obrazie w miejscu piksela o współrzędnych x,y, to sprawdzamy, czy współrzędna z tego punktu jest mniejsza od współrzędnej z zapisanej dotychczas w z-buforze w miejscu o współrzędnych x,y. Jeżeli tak, to rozpatrywany punkt leży bliżej niż punkt sceny, którego barwa została zapisana wcześniej w pamięci obrazu i zastępujemy dotychczasową barwę piksela x,y barwą rozpatrywanego punktu oraz zmieniamy dotychczasową wartość współrzędnej z na wartość współrzędnej z rozpatrywanego punktu. W przeciwnej sytuacji pozostawiamy poprzednią wartość piksela x,y oraz poprzednią wartość współrzędnej z. Sposób postępowania ilustruje rysunek VII.5. Proces powtarza się dla wszystkich wielokątów występujących w scenie (w bryle widzenia) i wszystkich punktów tych wielokątów, które potencjalnie mogą być odwzorowane na piksele w pamięci obrazu.

Rys. VII.5. Ilustracja metody z-bufora. a) Analiza wielokątów sceny, b) zawartość pamięci obrazu i z-bufora w kolejnych krokach. Wielokąty są analizowane w kolejności zielony, niebieski, żółty

W przypadku gdyby w scenie występował obiekt przezroczysty (bliższy od obiektów nieprzezroczystych), najpierw trzeba wykonać analizę obiektów nieprzezroczystych a dopiero potem analizę obiektu przezroczystego. Przy kilku obiektach przezroczystych powinny być one analizowane w kolejności od najdalszego do najbliższego.

Połączenie koloru obiektu nieprzezroczystego z kolorem obiektu przezroczystego można zrealizować korzystając z zależności

$$c_0=α_sc_s+(1-α_s)c_d$$

gdzie α;_s to współczynnik przezroczystości w zakresie (0,1), $c_s$ to kolor obiektu przezroczystego a $c_d$ to kolor obiektu nieprzezroczystego.

Rzutowanie

Zastanówmy się teraz w jaki sposób można przygotowaną scenę 3D odwzorować na płaszczyźnie ekranu. Problem ten oczywiście jest znany od dawna i wymyślono wiele różnych sposobów rzutowania. Niektóre z nich zaadaptowano dla potrzeb grafiki komputerowej. Dalej omówimy dwie najczęściej wykorzystywane metody rzutowania: rzutowanie perspektywiczne oraz rzutowanie równoległe.

W rzutowaniu perspektywicznym zakłada się, że obserwator znajduje się w pewnej odległości d przed ekranem oraz że wszystkie promienie rzutujące przecinają się w „oku” obserwatora. Oznacza to, że na początku trzeba całą scenę przenieść do układu współrzędnych, w którym osie x,y leżą w płaszczyźnie ekranu a oś z jest do niej prostopadła. Z kolei, dla znalezienia rzutu punktu leżącego w przestrzeni 3D na ekran, należy przez ten punkt poprowadzić promień rzutujący, który będzie również przechodził przez punkt, w którym znajduje się obserwator. Punkt, w którym promień rzutujący przetnie ekran (rzutnię) jest poszukiwanym rzutem punktu z przestrzeni 3D. Poglądowo wyjaśnia to rysunek VII.6.

Rys. VII.6. Zasada rzutowania perspektywicznego. Rzutem punktu A jest punkt A’

Przy obliczaniu współrzędnych rzutu punktu można korzystać z odpowiedniej macierzy we współrzędnych jednorodnych, podobnie jak w przypadku przekształceń geometrycznych. Odpowiednia macierz ma następującą postać:

Korzystając z tej postaci macierzy dla rzutu perspektywicznego należy pamiętać, że obowiązuje ona wtedy gdy dla rzutni $z=0$ a obserwator (środek rzutowania) jest w punkcie $z=-d$. Można również korzystać z macierzy uwzględniających dodatkowo obcinanie przez bryłę widzenia.

Przy rzutowaniu równoległym promienie rzutujące są do siebie równoległe. Jeżeli dodatkowo są one prostopadłe do rzutni, to mamy do czynienia z tak zwanym rzutem równoległym prostokątnym albo inaczej z rzutem ortogonalnym.

W rzucie ortogonalnym jeżeli oś z jest prostopadła do rzutni i dla rzutni $z=0$, to po zrzutowaniu punktu A(x,y,z) otrzymujemy punkt A’(x,y,0). Rysunek VII.7 ilustruje koncepcję rzutowania ortogonalnego.

Rys. VII.7. Rzut ortogonalny. Rzutem punktu A jest punkt A’

Rzuty ortogonalne są wykorzystywane często do pokazywania trzech widoków jakiegoś obiektu: widoku z przodu, widoku z boku i widoku z góry. Na rysunku VII.8 pokazano przykładowy obiekt w rzucie perspektywicznym (na dole z prawej strony) oraz trzy jego widoki ortogonalne.

Rys. VII.8. Obiekt (d) i jego rzuty ortogonalne: a) z przodu, b) z góry c) z prawej strony

Rasteryzacja

W praktyce, obliczenia związane z obiektami 3D w czasie renderingu w porządku obiektowych, z reguły są przez dłuższy czas wykonywane w odniesieniu do wierzchołków brył bądź węzłów siatek przybliżających powierzchnie brył. Same bryły bądź trójkąty (wielokąty) siatek są odtwarzane dopiero w końcowej fazie obliczeń związanych z rasteryzacją. Stąd, często podejście obiektowe jest określane również jako rendering rasteryzacyjny. Dodajmy, że pikselom dla których nie zostanie wyznaczona barwa w wyniku obliczeń związanych z poszczególnymi obiektami, jest przypisywana barwa, umownie określana jako barwa tła.

Metoda rzucania promieni

Ideę metody rzucania promieni ilustruje rysunek VII.9.

Rys. VII.9. Metoda rzucania promieni

Jak widać w stronę sceny zawierającej kilka obiektów puszczany jest promień z oka obserwatora (kamery) i przechodzący przez wybrany piksel. Na drodze promienia znajduje się pierwszy napotkany obiekt oraz punkt przecięcia promienia z tym obiektem. Przed wyznaczeniem barwy trafionego punktu powierzchni sprawdza się czy ten punkt jest bezpośrednio oświetlany przez źródła światła czy też znajduje się w cieniu. Sprawdzenie to polega na tym, że z analizowanego punktu wypuszcza się pomocnicze promienie (tak zwane promienie cieni) w kierunku źródeł światła. Jeżeli promień taki dotrze bezpośrednio do źródła światła, to światło to bezpośrednio oświetla analizowany punkt i wpływ tego światła uwzględnia się przy wyznaczaniu barwy punktu. Jeżeli natomiast taki promień nie dotrze do źródła światła wskutek trafienia po drodze na inny obiekt sceny, to przyjmuje się, że analizowany punkt leży w cieniu rzucanym przez ten obiekt i nie uwzględnia się wpływu takiego źródła na barwę punktu. Wyznaczona ostatecznie barwa analizowanego punktu powierzchni jest przypisywana pikselowi związanemu z rozpatrywanym promieniem.

Metoda śledzenia promieni

Cechą charakterystyczną opisanej wyżej metody rzucania promieni jest to, że przy wyznaczaniu barwy punktu powierzchni uwzględnia się tylko wpływ źródeł światła z których promienie docierają bezpośrednio do tego punktu. Natomiast metoda śledzenia promieni umożliwia znacznie dokładniejsze wyznaczanie barwy punktu powierzchni, dzięki temu, że umożliwia dodatkowo uwzględnienie wpływu sąsiednich obiektów na końcową barwę piksela.

W metodzie śledzenia promieni wyróżnia się dwie fazy obliczeń. W pierwszej fazie, podobnie jak w metodzie rzucania promieni, wypuszcza się z oka obserwatora promień w stronę sceny i przechodzący przez konkretny piksel ekranu. Promień ten po napotkaniu pierwszego obiektu odbija się i biegnie do momentu napotkania kolejnego obiektu. Tam ponownie promień zostaje odbity i biegnie do następnego najbliższego obiektu itd.

W trakcie analizy toru promienia można napotkać obiekt półprzezroczysty. Wtedy promień może zostać częściowo załamany i częściowo odbity. To, jaka część światła jest odbijana a jaka jest załamana opisują równania Fresnela. Kąt pod którym biegnie dalej promień załamany można określić z prawa załamania światła Snella. Kąt promienia odbitego jest równy kątowi promienia padającego. Każdy z tych dwóch promieni może być dalej niezależnie propagowany. Ilustruje to rysunek VII.10.

Rys. VII.10. Przykładowy bieg promienia w metodzie śledzenia promieni

Teoretycznie, proces ten można kontynuować dopóki promienie nie trafią do źródeł światła znajdujących się w scenie. W praktyce, proces śledzenia ogranicza się do kilku kolejnych odbić. W efekcie, uzyskuje się drzewo reprezentujące rozchodzenie się promienia trafiającego w scenę po przejściu przez analizowany piksel.

W drugiej fazie metody śledzenia promieni wyznacza się barwę jaką należy przypisać pikselowi. W tym celu najpierw wyznacza się barwy punktów ostatnio trafionych obiektów. Następnie wyznacza się barwy dla punktów obiektów znajdujących się wcześniej w strukturze drzewa. Uwzględnia się przy tym wpływ barw punktów wcześniej wyznaczonych itd. Dzięki takiemu postępowaniu, barwa punktu która będzie przypisana pikselowi będzie uzależniona zarówno od bezpośredniego oświetlenia przez źródła światła znajdujące się w scenie jak też oświetlenia pośredniego pochodzącego od sąsiednich obiektów. W przykładzie z rysunku VII.10 oznacza to, że najpierw powinniśmy wyznaczyć barwę punktu na powierzchni obiektu C, potem barwę punktu na powierzchni B (z uwzględnieniem wpływu promienia załamanego) i dopiero na końcu barwę punktu na powierzchni A (por. rysunek VII.11).

Rys. VII.11. Wyznaczanie barwy piksela w metodzie śledzenia promieni

Metoda śledzenia promieni jest bardzo efektywna jeśli chodzi o jakość uzyskiwanych obrazów. Obrazy uzyskiwane za pomocą tej metody są często określane mianem fotorealistycznych - ich jakość niejednokrotnie nie odbiega od jakości dobrych zdjęć.

Jednak istotnym ograniczeniem metody śledzenia promieni jest jej duża złożoność obliczeniowa. Liczba promieni wymagających analizy jest równa liczbie pikseli obrazu. Szukając sposobów przyspieszenia działania metody zbadano, które obliczenia związane z realizacją metody są najbardziej pracochłonne. Okazało się, że większość czasu zajmują obliczenia związane z wyznaczaniem przecięć promieni z obiektami i poszukiwaniem pierwszego napotkanego obiektu. Wiedząc o tym opracowano kilka sposobów zmniejszania nakładów obliczeniowych.

Jeden z najczęściej stosowanych sposobów polega na tym, że złożone obiekty występujące w scenie wstępnie otacza się bryłami, dla których łatwo sprawdza się przecięcie z promieniem. Są to najczęściej kule albo sześciany. Jeżeli trzeba sprawdzić czy promień przecina dany obiekt, to najpierw sprawdza się czy przecina on otaczającą kulę. Jeżeli nie, to nie podejmuje się próby przecinania promienia z obiektem. Dopiero jeżeli promień przetnie kulę, to wchodzi się w pracochłonną procedurę znalezienia przecięcia promienia z obiektem (oczywiście mimo wszystko wynik może być negatywny).

Inny sposób polega na tym, że całą scenę otacza się prostopadłościanem. Następnie prostopadłościan jest dzielony na pewną liczbę mniejszych prostopadłościanów. Z kolei, dla każdego takiego mniejszego prostopadłościanu, określa się listę obiektów sceny, które w całości lub częściowo należą do niego. Analizując teraz bieg promienia można znaleźć te mniejsze prostopadłościany, przez które przechodzi promień i w dalszych obliczeniach można się ograniczyć tylko do obiektów, które są związane z wybranymi prostopadłościanami. Z pozostałymi obiektami promień na pewno nie przetnie się. Metodę tę poglądowo wyjaśnia rysunek VII.12, na którym dla uproszczenia pokazano przypadek dwuwymiarowy. Oczywiście możliwe jest połączenie obu sposobów. Obiekty przypisywane poszczególnym mniejszym prostopadłościanów mogą być na początku otoczone pomocniczymi bryłami (kulami)

Rys. VII.12. Poglądowe wyjaśnienie metody podziału przestrzeni sceny na prostopadłościany

Przecięcie promień - kula

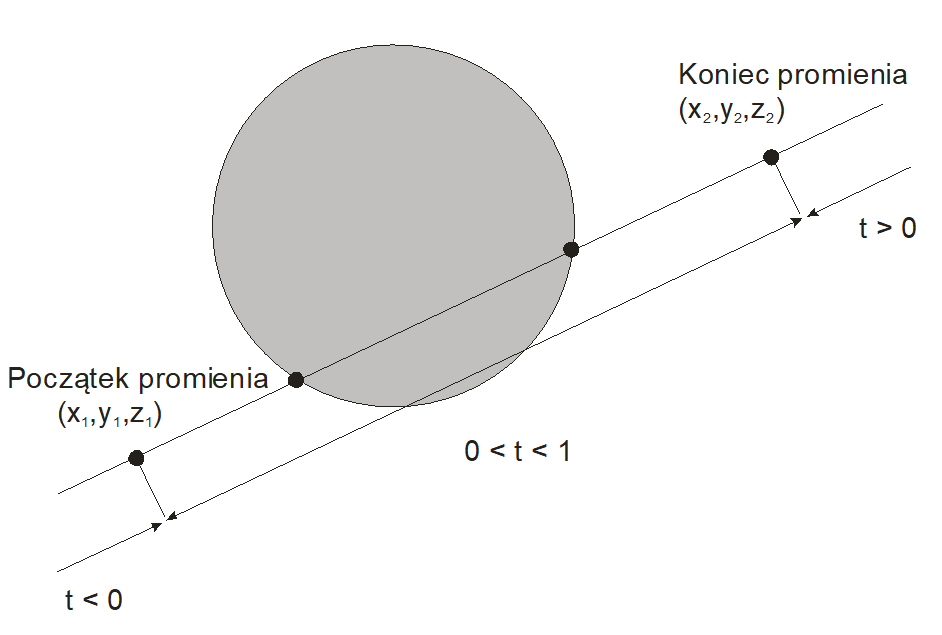
Rys. VII.13. Przecięcie promienia z kulą

Przypomnijmy, że równanie kuli o promieniu r i środku w punkcie $(l, m, n)$ ma postać

$$(x-l)^2+(y-m)^2+(z-n)^2=r^2$$

Równania parametryczne, dla $0≤t≤1$, opisujące promień zaczynający się w punkcie $(x_1,y_1,z_1)$ i kończący się w punkcie $(x_2,y_2,z_2)$ (por. rys. VII.13) można zapisać w postaci

$$x=x_1+(x_2-x_1)t=x_1+it$$ $$y=y_1+(y_2-y_1)t=y_1+jt$$ $$z=z_1+(z_2-z_1)t=z_1+kt$$

Po podstawieniu równań promienia do równania kuli i uporządkowaniu otrzymuje się równanie kwadratowe. Po znalezieniu Δ można stwierdzić czy promień przecina kulę, jest styczny do kuli albo czy nie przecina kuli. W przypadku przecinania kuli trzeba wybrać rozwiązanie reprezentujące punkt bliższy początkowi promienia.

Przecięcie promień - trójkąt

Przypomnijmy, że dla sprawdzenia czy punkt P należy do trójkąta o znanych wierzchołkach (A,B,C) można wyznaczyć współrzędne barycentryczne punktu. Jeżeli wszystkie współrzędne będą dodatnie to punkt należy do trójkąta.

Równanie promienia o początku w punkcie o można zapisać w postaci (por. rys. VII.14)

$$\bi r(t)=\bi o+t\bi d$$

gdzie d jest wektorem kierunkowym, zwykle jednostkowym.

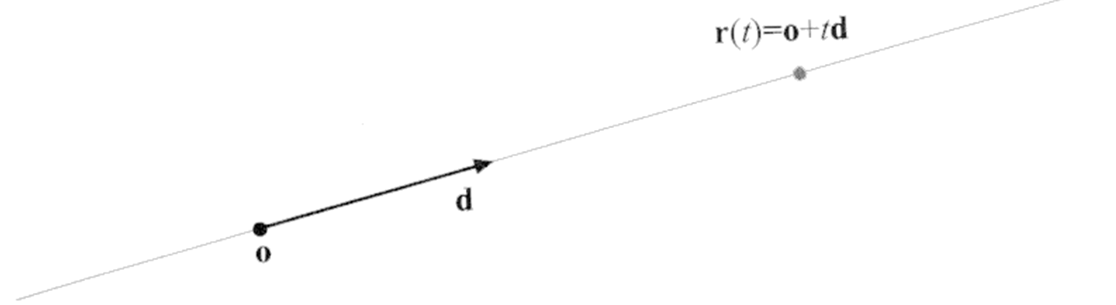
Rys. VII.14. Ilustracja sposobu opisywania promienia

Punkt P musi należeć do promienia (dla określonej wartości t). Stąd otrzymuje się układ trzech równań z trzema niewiadomymi α,β,t

$$\bi o+t\bi d=α\bi A+β\bi B+(1-α-β)\bi C$$